题目内容
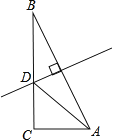
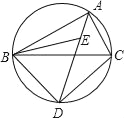
【题目】如图:△ABC是圆的内接三角形,∠BAC与∠ABC的角平分线AE、BE相交于点E,延长AE交圆于点D,连接BD、DC,且∠BCA=60°.
(1)求证:△BED为等边三角形;
(2)若∠ADC=30°,⊙O的半径为2![]() ,求BD长.
,求BD长.
【答案】(1)见解析;(2)4.
【解析】
(1)根据角平分线的定义、三角形内角和定理得到∠DEB=60°,根据圆周角定理得到∠BDA=∠BCA=60°,根据等边三角形的判定定理证明;
(2)根据圆周角定理得到BC是⊙O的直径,根据勾股定理计算即可.
(1)证明:∵∠BAC与∠ABC的角平分线AE、BE相交于点E,
∴∠EAB=![]() ∠CAB,∠EBA=
∠CAB,∠EBA=![]() ∠CBA,
∠CBA,
∴∠AEB=180°﹣(∠EAB+∠EBA)=180°﹣(![]() ∠CAB+
∠CAB+![]() ∠CBA)=180°﹣
∠CBA)=180°﹣![]() (180°﹣∠BCA)=120°,
(180°﹣∠BCA)=120°,
∴∠DEB=60°,
由圆周角定理得,∠BDA=∠BCA=60°,
∴△BED为等边三角形;
(2)∵∠ADC=30°,∠BDA=60°,
∴∠BDC=90°,
∴BC是⊙O的直径,即BC=4![]() ,
,
∵AE平分∠BAC,
∴![]() =
=![]() ,
,
∴BD=DC=4.

练习册系列答案
相关题目