题目内容
在梯形ABCD中,AD∥BC,AB⊥AD,AB=4,AD=5,CD=5.E为底边BC上一点,以点E为圆心, BE为半径画⊙E交线段DE于点F.
BE为半径画⊙E交线段DE于点F.
(1)如图,当点F在线段DE上时,设BE=x,DF=y,试建立y关于x的函数关系式,并写出自变量x的取值范围;
(2)当以CD为直径的⊙O与⊙E相切时,求x的值;
(3)连接AF、BF,当△ABF是以AF为腰的等腰三角形时,求x的值.
 BE为半径画⊙E交线段DE于点F.
BE为半径画⊙E交线段DE于点F.(1)如图,当点F在线段DE上时,设BE=x,DF=y,试建立y关于x的函数关系式,并写出自变量x的取值范围;
(2)当以CD为直径的⊙O与⊙E相切时,求x的值;
(3)连接AF、BF,当△ABF是以AF为腰的等腰三角形时,求x的值.
(1)如图1,过点D作DG⊥BC于点G.
可得DG=AB=4,BG=AD,GC=3,BC=8,EG=5-x;
在Rt△DEG中,
∴DE2=EG2+DG2,即(x+y)2=42+(5-x)2;
∴y=
-x(负值舍去)
定义域:0<x≤4.1;
(2)设CD的中点O,连接EO,过点O作OH⊥BC于点H.
OC=
,OH=2,HC=
,EH=8-x-
;
①⊙O与⊙E外切时,OE=x+
在Rt△OEH中,OE2=OH2+EH2,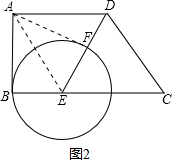
∴22+(8-x-
)2=(x+
)2
∴4+x2-13x+
=x2+5x+
,
∴18x=40,
化简并解得x=
;
②⊙O与⊙E内切时,OE=|x-
|
在Rt△OEH中,OE2=OH2+EH2,
∴22+(8-x-
)2=(x-
)2,
∴4+x2-13x+
=x2-5x+
,
∴8x=40,
化简并解得x=5;
综上所述,当⊙O与⊙D相切时,x=5或
;
(3)如图2,连接AF,AE,
当AF=AB=4时,由BE=EF,AE=AE,有△ABE和△AEF全等,
∴∠AFE=∠ABE=90°,即AF⊥DE
在Rt△AFD中,DF=
=3;
由y=
-x=3,解得x=2;
如图3,当FA=FB时,过点F作QF⊥AB于点Q,有AQ=BQ,且AD∥BC∥FQ,
∴DF=EF,y=
-x=x,x=
(负值舍去);
综上所述,当△ABF是以AF为腰的等腰三角形时,
x=2或
.

可得DG=AB=4,BG=AD,GC=3,BC=8,EG=5-x;
在Rt△DEG中,
∴DE2=EG2+DG2,即(x+y)2=42+(5-x)2;
∴y=
| (5-x)2+16 |
定义域:0<x≤4.1;
(2)设CD的中点O,连接EO,过点O作OH⊥BC于点H.
OC=
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
①⊙O与⊙E外切时,OE=x+
| 5 |
| 2 |
在Rt△OEH中,OE2=OH2+EH2,

∴22+(8-x-
| 3 |
| 2 |
| 5 |
| 2 |
∴4+x2-13x+
| 169 |
| 4 |
| 25 |
| 4 |
∴18x=40,
化简并解得x=
| 20 |
| 9 |
②⊙O与⊙E内切时,OE=|x-
| 5 |
| 2 |
在Rt△OEH中,OE2=OH2+EH2,
∴22+(8-x-
| 3 |
| 2 |
| 5 |
| 2 |
∴4+x2-13x+
| 169 |
| 4 |
| 25 |
| 4 |
∴8x=40,
化简并解得x=5;
综上所述,当⊙O与⊙D相切时,x=5或
| 20 |
| 9 |
(3)如图2,连接AF,AE,
当AF=AB=4时,由BE=EF,AE=AE,有△ABE和△AEF全等,
∴∠AFE=∠ABE=90°,即AF⊥DE
在Rt△AFD中,DF=
| AD2-AF2 |

由y=
| (5-x)2+16 |
如图3,当FA=FB时,过点F作QF⊥AB于点Q,有AQ=BQ,且AD∥BC∥FQ,
∴DF=EF,y=
| (5-x)2+16 |
-5±2
| ||
| 3 |
综上所述,当△ABF是以AF为腰的等腰三角形时,
x=2或
-5+2
| ||
| 3 |


练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目




 △CPQ进行研究.
△CPQ进行研究.


