题目内容
【题目】如图所示,已知在平行四边形ABCD中,BE=DF.求证:∠DAE=∠BCF. 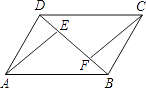
【答案】证明:∵四边形ABCD为平行四边形, ∴AD∥BC,且AD=BC,
∴∠ADE=∠CBF
又∵BE=DF,
∴BF=DE,
∵在△ADE和△CBF中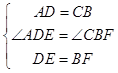 ,
,
∴△ADE≌△CBF(SAS),
∴∠DAE=∠BCF.
【解析】根据平行四边形性质求出AD∥BC,且AD=BC,推出∠ADE=∠CBF,求出DE=BF,证△ADE≌△CBF,推出∠DAE=∠BCF即可.
【考点精析】掌握平行线的性质和平行四边形的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目