ЬтФПФкШн
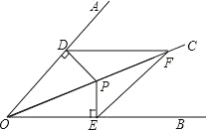
ЁОЬтФПЁПКўжнЫигагуУзжЎЯчжЎГЦЃЌФГЫЎВњбјжГДѓЛЇЮЊСЫИќКУЕиЗЂЛгММЪѕгХЪЦЃЌвЛДЮадЪеЙКСЫ ![]()
![]() ЕЫЎгуЃЌМЦЛЎбјжГвЛЖЮЪБМфКѓдйГіЪлЃЎвбжЊУПЬьЗХбјЕФЗбгУЯрЭЌЃЌЗХбј
ЕЫЎгуЃЌМЦЛЎбјжГвЛЖЮЪБМфКѓдйГіЪлЃЎвбжЊУПЬьЗХбјЕФЗбгУЯрЭЌЃЌЗХбј ![]() ЬьЕФзмГЩБОЮЊ
ЬьЕФзмГЩБОЮЊ ![]() ЭђдЊЃЛЗХбј
ЭђдЊЃЛЗХбј ![]() ЬьЕФзмГЩБОЮЊ
ЬьЕФзмГЩБОЮЊ ![]() ЭђдЊЃЈзмГЩБО=ЗХбјзмЗбгУ+ЪеЙКГЩБОЃЉЃЎ
ЭђдЊЃЈзмГЩБО=ЗХбјзмЗбгУ+ЪеЙКГЩБОЃЉЃЎ
ЃЈ1ЃЉЩшУПЬьЕФЗХбјЗбгУЪЧ ![]() ЭђдЊЃЌЪеЙКГЩБОЮЊ
ЭђдЊЃЌЪеЙКГЩБОЮЊ ![]() ЭђдЊЃЌЧѓ
ЭђдЊЃЌЧѓ ![]() КЭ
КЭ ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЩшетХњЕЫЎгуЗХбј ![]() ЬьКѓЕФжЪСПЮЊ
ЬьКѓЕФжЪСПЮЊ ![]() ЃЈ
ЃЈ ![]() ЃЉЃЌЯњЪлЕЅМлЮЊ
ЃЉЃЌЯњЪлЕЅМлЮЊ ![]() дЊ/
дЊ/ ![]() ЃЎИљОнвдЭљОбщПЩжЊЃК
ЃЎИљОнвдЭљОбщПЩжЊЃК ![]() гы
гы ![]() ЕФКЏЪ§ЙиЯЕЮЊ
ЕФКЏЪ§ЙиЯЕЮЊ ![]() ЃЛ
ЃЛ ![]() гы
гы ![]() ЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ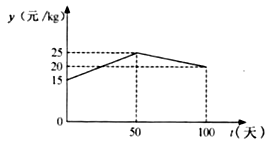
ЂйЗжБ№ЧѓГіЕБ ![]() КЭ
КЭ ![]() ЪБЃЌ
ЪБЃЌ ![]() гы
гы ![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЩшНЋетХњЕЫЎгуЗХбј ![]() ЬьКѓвЛДЮадГіЪлЫљЕУРћШѓЮЊ
ЬьКѓвЛДЮадГіЪлЫљЕУРћШѓЮЊ ![]() дЊЃЌЧѓЕБ
дЊЃЌЧѓЕБ ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ ![]() зюДѓЃПВЂЧѓГізюДѓжЕЃЎЃЈРћШѓ=ЯњЪлзмЖю-змГЩБОЃЉ
зюДѓЃПВЂЧѓГізюДѓжЕЃЎЃЈРћШѓ=ЯњЪлзмЖю-змГЩБОЃЉ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКвРЬтПЩЕУЃК ![]()
НтЕУ ![]()
Д№ЃКaЕФжЕЮЊ0.04ЃЌbЕФжЕЮЊ30.
ЃЈ2ЃЉ
НтЃКЂйЕБ0ЁмtЁм50ЪБЃЌЩшyгыtЕФКЏЪ§ЙиЯЕЪНЮЊy=k1t+n1.
АбЕуЃЈ0ЃЌ15ЃЉЃЌЃЈ50ЃЌ25ЃЉЕФзјБъЗжБ№ДњШыЕУ:![]()
НтЕУ: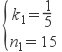
ЁрyгыtЕФКЏЪ§ЙиЯЕЪНЮЊy=![]() t+15.
t+15.
ЕБ50ЃМtЁм100ЪБЃЌЩшyгыtЕФКЏЪ§ЙиЯЕЪНЮЊy=k2t+n2.
АбЕуЃЈ50ЃЌ25ЃЉКЭЃЈ100ЃЌ20ЃЉЕФзјБъЗжБ№ДњШыЕУ :![]()
НтЕУ :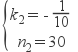
ЁрyгыtЕФКЏЪ§ЙиЯЕЪНЮЊy=-![]() t+30.
t+30.
ЂкгЩЬтвтЕУЃЌЕБ0ЁмtЁм50ЪБЃЌ
W=20000ЁСЃЈ![]() t+15ЃЉ-ЃЈ400t+300000ЃЉ=3600t
t+15ЃЉ-ЃЈ400t+300000ЃЉ=3600t
Ёп3600ЃО0ЃЌЁрЕБt=50ЪБЃЌWзюДѓжЕ=180000ЃЈдЊЃЉ
ЕБ50ЃМtЁм100ЪБЃЌW=ЃЈ100t+15000ЃЉ(-![]() t+30ЃЉ-ЃЈ400t+300000ЃЉ=-10t2+1100t+150000=-10ЃЈt-55ЃЉ2+180250
t+30ЃЉ-ЃЈ400t+300000ЃЉ=-10t2+1100t+150000=-10ЃЈt-55ЃЉ2+180250
Ёп-10ЃМ0ЃЌЁрЕБt=55ЪБЃЌWзюДѓжЕ=180250
злЩЯЫљЪіЃЌЕБtЮЊ55ЬьЪБЃЌWзюДѓЃЌзюДѓжЕЮЊ180250дЊ.
ЁОНтЮіЁПЃЈ1ЃЉИљОнЬтвтЃЌСаЗНГЬзщЧѓНтМДПЩ.
ЃЈ2ЃЉЭЈЙ§ЭМЯёевЕНЯргІЕФЕуЕФзјБъЃЌИљОнД§ЖЈЯЕЪ§ЗЈЗжРрСаГіЗНГЬзщМДПЩЕУЕНКЏЪ§НтЮіЪНЃЛШЛКѓИљОнРћШѓ=ЯњЪлзмЖю-змГЩБО=ЯњЪлЕЅМлЁСЯњЪлЬьЪ§-ЃЈЗХбјзмЗбгУ+ЪеЙКГЩБОЃЉЃЌШЛКѓИљОнвЛДЮКЏЪ§ЕФЬиЕуКЭЖўДЮКЏЪ§ЕФзюжЕЧѓНтМДПЩ.
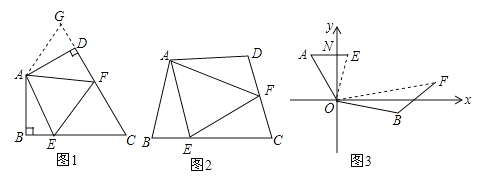
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫНтЖўдЊвЛДЮЗНГЬзщКЭШЗЖЈвЛДЮКЏЪ§ЕФБэДяЪНЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮеЖўдЊвЛДЮЗНГЬзщЃКЂйДњШыЯћдЊЗЈЃЛЂкМгМѕЯћдЊЗЈЃЛШЗЖЈвЛИівЛДЮКЏЪ§ЃЌашвЊШЗЖЈвЛДЮКЏЪ§ЖЈвхЪНy=kx+bЃЈkВЛЕШгк0ЃЉжаЕФГЃЪ§kКЭbЃЎНтетРрЮЪЬтЕФвЛАуЗНЗЈЪЧД§ЖЈЯЕЪ§ЗЈВХФме§ШЗНтД№ДЫЬтЃЎ