题目内容
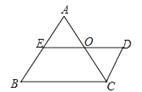
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.
(1)求证:OD=OC;
(2)若∠AOB=60°,求证:OE=4EF.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)利用角平分线定理得到ED=EC,再由斜边为公共边,利用HL得到直角三角形ODE与直角三角形OCE全等,利用全等三角形的对应边相等即可得证;
(2)由OE为角平分线,且∠AOB=60°,得到∠DOE=∠EDF=30°,在直角三角形ODE中,利用30度角所对的直角边等于斜边的一半得到OE=2DE,在直角三角形DEF中,利用30度角所对的直角边等于斜边的一半得到DE=2EF,等量代换即可得证.
证明:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴ED=EC,
在Rt△ODE和Rt△OCE中,
![]() ,
,
∴Rt△ODE≌Rt△OCE(HL),
∴OD=OC;
(2)∵∠AOB=60°,OE平分∠AOB,
∴∠DOE=∠COE=30°,
∴∠DEO=60°,∠EDF=30°,
∵在Rt△ODE中,∠DOE=30°,
∴OE=2DE,
∵在Rt△DEF中,∠EDF=30°,
∴DE=2EF,
∴OE=4EF.

 阅读快车系列答案
阅读快车系列答案【题目】绵阳农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了50个谷穗作为样本,量得它们的长度(单位:cm).对样本数据适当分组后,列出了如下频数分布表:
穗长 | 4.5≤x<5 | 5≤x<5.5 | 5.5≤x<6 | 6≤x<6.5 | 6.5≤x<7 | 7≤x<7.5 |
频数 | 4 | 8 | 12 | 13 | 10 | 3 |
(1)在图1、图2中分别出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;并计算出这块试验田里穗长在5.5≤x<7范围内的谷穗所占的百分比.
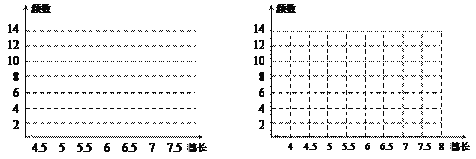
图1 图2