Question

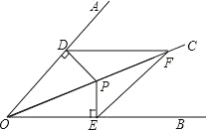
【题目】如图， OC 是AOB 的平分线， P 是OC 上的一点， PD OA 于 D ，PE OB 于 E ． F 是OC 上的另一点，连接 DF 、 EF ．

（1）求证： DPF EPF ；

（2）比较 DF 与 EF 的大小关系，并说明理由．

Answer 1

【答案】（1）详见解析；（2）DF=EF，理由详见解析.

【解析】

（1）先根据角平分线的性质可以得出PD=PE，就可以得出△PDO≌△PEO，就可以得出OPD OPE，进而证明DPF EPF ；

（2）根据（1）中△PDO≌△PEO，根据全等三角形的性质得到，OD=OE，∠POD=∠POE，证明△DOF≌△EOF，就可以得出结论．

证明：（1）∵OC是∠AOB的角平分线，PD⊥OA，PE⊥OB，

∴PD=PE.

在Rt△PDO和Rt△PEO中，

∴Rt△PDO≌Rt△PEO(HL)，

OPD OPE，

∴DPF EPF ；

（2）DF=EF.

理由如下：Rt△PDO≌Rt△PEO(HL)，

∴OD=OE，∠POD=∠POE.

在△DOF和△EOF中，

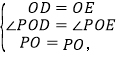
∴△DOF≌△EOF(SAS)，

∴DF=EF.