题目内容
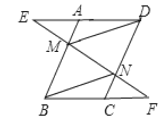
【题目】说理填空：如图，点E是DC的中点，EC=EB，∠CDA=120°，DF//BE，且DF平分∠CDA，若△BCE的周长为18cm，求DC的长．
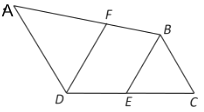
解： 因为DF平分∠CDA,（已知）
所以∠FDC=
∠_________.（____________________）
因为∠CDA=120°,（已知）所以∠FDC=______°.
因为DF//BE,（已知）
所以∠FDC=∠_________=60°.（____________________________________）
又因为EC=EB,（已知）
所以△BCE为等边三角形.（________________________________________）
因为△BCE的周长为18cm,（已知） 所以BE=EC=BC=6 cm.
因为点E是DC的中点,（已知） 所以DC=2EC=12 cm .
【答案】ADC；角平分线意义；60；BEC；两直线平行，同位角相等；有一个角是60°的等腰三角形是等边三角形
【解析】
利用角平分线的性质得出∠FDC的度数，再利用平行线的性质得出∠BEC的度数，进而得出△BCE为等边三角形．
∵DF平分∠CDA，（已知）
∴∠FDC=
∠ADC．（角平分线意义）
∵∠CDA=120°，（已知）
∴∠FDC=60°．
∵DF∥BE，（已知）
∴∠FDC=∠BEC=60°．（两直线平行，同位角相等）
又∵EC=EB，（已知）
∴△BCE为等边三角形．（有一个角是60°的等腰三角形是等边三角形）
∵△BCE的周长为18cm，（已知）
∴BE=EC=BC=6cm．
∵点E是DC的中点，（已知）
∴DC=2EC=12cm．
练习册系列答案
相关题目
