题目内容
如图,已知双曲线 经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.
(1)k=6;(2) ;(3)根据题意求出点A、B的坐标,然后利用待定系数法求出直线AB的解析式,可知与直线CD的解析式k值相等,所以AB、CD平行.
;(3)根据题意求出点A、B的坐标,然后利用待定系数法求出直线AB的解析式,可知与直线CD的解析式k值相等,所以AB、CD平行.
解析试题分析:(1)把点D的坐标代入双曲线解析式,进行计算即可得解;
(2)先根据点D的坐标求出BD的长度,再根据三角形的面积公式求出点C到BD的距离,然后求出点C的纵坐标,再代入反比例函数解析式求出点C的坐标,然后利用待定系数法求一次函数解析式解答;
(3)根据题意求出点A、B的坐标,然后利用待定系数法求出直线AB的解析式,可知与直线CD的解析式k值相等,所以AB、CD平行.
解:(1)∵双曲线 经过点D(6,1),
经过点D(6,1),
∴ ,解得k=6;
,解得k=6;
(2)设点C到BD的距离为h,
∵点D的坐标为(6,1),DB⊥y轴,
∴BD=6,
∴S△BCD= ×6•h=12,
×6•h=12,
解得h=4,
∵点C是双曲线第三象限上的动点,点D的纵坐标为1,
∴点C的纵坐标为1-4=-3,
∴ ,解得x=-2,
,解得x=-2,
∴点C的坐标为(-2,-3),
设直线CD的解析式为y=kx+b,
所以,直线CD的解析式为 ;
;
(3)AB∥CD.理由如下:
∵CA⊥x轴,DB⊥y轴,设点C的坐标为(c, ),点D的坐标为(6,1),
),点D的坐标为(6,1),
∴点A、B的坐标分别为A(c,0),B(0,1),
设直线AB的解析式为y=mx+n,
所以,直线AB的解析式为y=- x+1,
x+1,
设直线CD的解析式为y=ex+f,
∴直线CD的解析式为y=- x+
x+ ,
,
∵AB、CD的解析式k都等于- ,
,
∴AB与CD的位置关系是AB∥CD.
考点:反比例函数的综合题
点评:本题是对反比例函数的综合考查,主要利用了待定系数法求函数解析式,三角形的面积的求解,待定系数法是求函数解析式最常用的方法,一定要熟练掌握并灵活运用.

(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
| | 空调 | 彩电 |
| 进价(元/台) | 5400 | 3500 |
| 售价(元/台) | 6100 | 3900 |
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
漳州三宝之一“水仙花”畅销全球,某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
| | A地 | B地 | C地 |
| 运费(元/件) | 20 | 10 | 15 |
(2)若总运费不超过12000元,最多可运往A地的水仙花多少件?
如图,已知二次函数 =
= ,当
,当 <
< <
< 时,
时,  随
随 的增大而增大,则实数a的取值范围是 ( )
的增大而增大,则实数a的取值范围是 ( )
A. > > | B. < < ≤ ≤ | C. >0 >0 | D. < < < < |
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论正确的是( )
| A.b2>4ac | B.ac>0 | C.a﹣b+c>0 | D.4a+2b+c<0 |
二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1).则代数式1-a-b的值为( )
| A.-3 | B.-1 | C.2 | D.5 |
将一条抛物线向左平移2个单位后得到了y=2x2的函数图象,则这条抛物线是( )
| A.y=2x2+2 | B.y=2x2-2 | C.y=2(x-2)2 | D.y=2(x+2)2 |
 ,点C的坐标为(-18,0).
,点C的坐标为(-18,0).
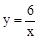 的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).