题目内容
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)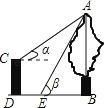
【答案】解:作CF⊥AB于点F,设AF=x米,
在Rt△ACF中,tan∠ACF= ![]() ,
,
则CF= ![]() =
= ![]() x,
x,
在直角△ABE中,AB=x+BF=4+x(米),
在直角△ABF中,tan∠AEB= ![]() ,则BE=
,则BE= ![]() =
= ![]() (x+4)米.
(x+4)米.
∵CF﹣BE=DE,即 ![]() x﹣
x﹣ ![]() (x+4)=3.
(x+4)=3.
解得:x= ![]() ,
,
则AB= ![]() +4=
+4= ![]() (米).
(米).
答:树高AB是 ![]() 米.
米.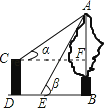
【解析】作CF⊥AB于点F,设AF=x米,在直角△ACF中利用三角函数用x表示出CF的长,在直角△ABE中表示出BE的长,然后根据CF﹣BE=DE即可列方程求得x的值,进而求得AB的长.本题考查了解直角三角形的应用,解答本题关键是构造直角三角形,利用三角函数的知识表示出相关线段的长度.
【考点精析】掌握关于仰角俯角问题是解答本题的根本,需要知道仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
【题目】甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:

根据以上信息,请解答下面的问题;
选手 | A平均数 | 中位数 | 众数 | 方差 |
甲 | a | 8 | 8 | c |
乙 | 7.5 | b | 6和9 | 2.65 |
(1)补全甲选手10次成绩频数分布图.
(2)a= ,b= ,c= .
(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).