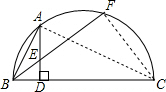
题目内容
如图所示,BC是⊙O直径,AD⊥BC,垂足为D,
=
,BF与AD交于E,求证:AE=BE.

 |
| BA |
 |
| AF |

证明:连CF,AC,
∵
=
,
∴∠BCA=∠ACF,∠ACF=∠ABF,
∵BC为圆的直径,∴∠BAC=90°,
∴∠ABC+∠ACB=90°,
又AD⊥BC,∴∠ADB=90°,
∴∠ABC+∠BAD=90°,
∴∠BAD=∠BCA,
∴∠ABF=∠BAD,
即BE=AE.
∵
 |
| BA |
 |
| AF |
∴∠BCA=∠ACF,∠ACF=∠ABF,
∵BC为圆的直径,∴∠BAC=90°,
∴∠ABC+∠ACB=90°,
又AD⊥BC,∴∠ADB=90°,
∴∠ABC+∠BAD=90°,
∴∠BAD=∠BCA,
∴∠ABF=∠BAD,
即BE=AE.


练习册系列答案
相关题目






