题目内容
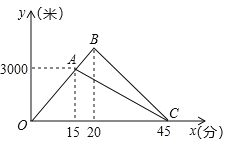
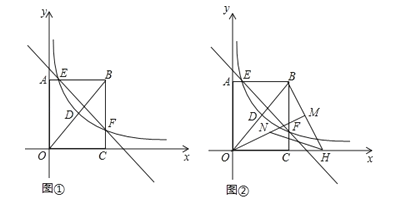
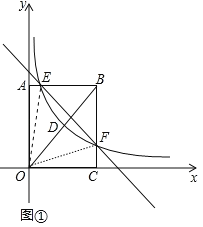
【题目】如图①,在矩形OABC中,OA=4,OC=3,分别以OC、OA所在的直线为x轴、y轴,建立如图所示的坐标系,连接OB,反比例函数y=![]() (x>0)的图象经过线段OB的中点D,并与矩形的两边交于点E和点F,直线l:y=kx+b经过点E和点F.
(x>0)的图象经过线段OB的中点D,并与矩形的两边交于点E和点F,直线l:y=kx+b经过点E和点F.
(1)写出中点D的坐标 ,并求出反比例函数的解析式;
(2)连接OE、OF,求△OEF的面积;
(3)如图②,将线段OB绕点O顺时针旋转一定角度,使得点B的对应点H恰好落在x轴的正半轴上,连接BH,作OM⊥BH,点N为线段OM上的一个动点,求HN+![]() ON的最小值.
ON的最小值.
【答案】(1)D(![]() ,2),y=
,2),y=![]() ;(2)
;(2)![]() ;(3)4.
;(3)4.
【解析】
(1)首先确定点B坐标,再根据中点坐标公式求出点D的坐标即可解决问题.
(2)求出点E,F的坐标,再根据S△OEF=S矩形ABCO﹣S△AOE﹣S△OCF﹣S△EFB计算即可.
(3)如图②中,作NJ⊥BD于J.HK⊥BD于K.解直角三角形首先证明:sin∠JOD=![]() ,推出NJ=ONsin∠NOD=
,推出NJ=ONsin∠NOD=![]() ON,推出NH+
ON,推出NH+![]() ON=NH+NJ,根据垂线段最短可知,当J,N,H共线,且与HK重合时,HN+
ON=NH+NJ,根据垂线段最短可知,当J,N,H共线,且与HK重合时,HN+![]() ON的值最小,最小值=HK的长,由此即可解决问题.
ON的值最小,最小值=HK的长,由此即可解决问题.
(1)在矩形ABCO中,∵OA=BC=4,OC=AB=3,
∴B(3,4).
∵OD=DB,
∴D(![]() ,2).
,2).
∵y=![]() 经过D(
经过D(![]() ,2),
,2),
∴k=3,
∴反比例函数的解析式为y=![]() .
.
(2)如图①中,连接OE,OF.
由题意E(![]() ,4),F(3,1),
,4),F(3,1),
∴S△OEF=S矩形ABCO﹣S△AOE﹣S△OCF﹣S△EFB=12﹣![]() ×4×
×4×![]() ﹣
﹣![]() ×3×1﹣
×3×1﹣![]() ×3×(3﹣
×3×(3﹣![]() )=
)=![]() .
.
(3)如图②中,作NJ⊥BD于J.HK⊥BD于K.

由题意OB=OH=5,
∴CH=OH﹣OC=5﹣3=2,
∴BH=![]() =2
=2![]() ,
,
∴sin∠CBH=![]() =
=![]() .
.
∵OM⊥BH,
∴∠OMH=∠BCH=90°.
∵∠MOH+∠OHM=90°,∠CBH+∠CHB=90°,
∴∠MOH=∠CBH.
∵OB=OH,OM⊥BH,
∴∠MOB=∠MOH=∠CBH,
∴sin∠JOD=![]() ,
,
∴NJ=ONsin∠NOD=![]() ON,
ON,
∴NH+![]() ON=NH+NJ,
ON=NH+NJ,
根据垂线段最短可知,当J,N,H共线,且与HK重合时,HN+![]() ON的值最小,最小值=HK的长.
ON的值最小,最小值=HK的长.
∵OB=OH,BC⊥OH,HK⊥OB,
∴HK=BC=4,
∴HN+![]() ON是最小值为4.
ON是最小值为4.