题目内容
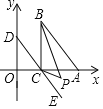
【题目】如图，点O（0,0），点B（0,1）是第一个正方形OBB1C的两个顶点，以它的对角线OB1为一边作第二个正方形OB1B2C1，以正方形OB1B2C1的对角线OB2为一边作第三个正方形OB2B3C2，再以正方形OB2B3C2的对角线OB3为一边作第四个正方形OB3B4C3…以此规律作下去，点B2014的坐标为______．
【答案】(-21007,0)
【解析】
根据题意和图形可看出每经过一次变化，都顺时针旋转45°，边长都乘以
，所以可求出从B到B3的后变化的坐标，再求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标，找出这些坐标的之间的规律，然后根据规律计算出点B2014的坐标．
根据题意和图形可看出每经过一次变化，都顺时针旋转45°，边长都乘以，
∵从B、B3经过了3次变化
∵
，
∴点B3所在的正方形的边长为
，点B3位置在第四象限
∴点B3的坐标是(2,2)
可得出：B1点坐标为(1,1)
B2点坐标为(0,2)
B3点坐标为(2,2)
B4点坐标为(0,4)
B5点坐标为(4,4)
B6(8,0)，B7(8,8)，B8(0,16)，B9(16,16)
由规律可以发现，每经过8次作图后，点的坐标符号与第一次坐标符号相同，每次正方形的边长变为原来的倍
∵2014÷8=251…6
∴B2014的纵横坐标符号与点B6的相同，横坐标为负值，纵坐标为0
∴B2014的坐标为(21007,0)
故答案为：(21007,0)
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
【题目】下表数据是科研小组在某地区根据调查获取的：“距离地面的高度（千米）与此处的温度（摄氏度）”的关系。
距离地面高度/千米 | 0 | 1 | 2 | 3 | 4 | 5 |
温度/摄氏度 | 20 | 14 | 8 | 2 | -4 | -10 |
根据上表，请你回答：
（1）上表中___________是自变量；_________________是因变量；
（2）如果用
表示距离地面的高度（千米），
表示温度（摄氏度），请你写出与的关系式____________________________________；
（3）请你利用（2）的结论，求该地区：①距离地面6.2千米的高空温度是多少？②当高空某处温度为-52度时，该处的高度是多少？
