题目内容
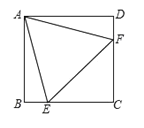
【题目】如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F.求证:(1)△ACE≌△BCD;(2)![]() .
.

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)由三角形ABC与三角形CDE都为等边三角形,利用等边三角形的性质得到两对边相等,一对角相等,利用等式的性质得到夹角相等,利用SAS即可得证;
(2)由(1)得出的三角形全等得到对应角相等,再由一对角相等,且夹边相等,利用ASA得到三角形GCD与三角形FCE全等,利用全等三角形对应边相等得到CG=CF,进而确定出三角形CFG为等边三角形,确定出一对内错角相等,进而得到GF与CE平行,利用平行线等分线段成比例即可得证.
试题解析:解:(1)∵△ABC与△CDE都为等边三角形,∴AC=BC,CE=CD,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD.在△ACE和△BCD中,∵AC=BC,∠ACE=∠BCD,CE=CD,∴△ACE≌△BCD(SAS);
(2)∵△ACE≌△BCD,∴∠BDC=∠AEC.在△GCD和△FCE中,∵∠GCD=∠FCE=60°,CD=CE,∠BDC=∠AEC,∴△GCD≌△FCE(ASA),∴CG=CF,∴△CFG为等边三角形,∴∠CGF=∠ACB=60°,∴GF∥CE,∴ ![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目