题目内容
【题目】观察、猜想、探究:
在△ABC中,![]() .
.
(1)如图①,当![]() ,AD为∠BAC的角平分线时,求证:
,AD为∠BAC的角平分线时,求证:![]() ;
;
(2)如图②,当![]() ,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的
,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的
数量关系?请写出你的猜想,并对你的猜想给予证明;
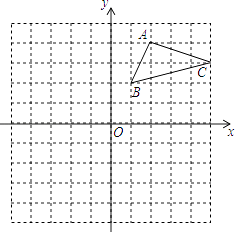
(3)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想.



【答案】(1)见解析;(2 ) ![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】试题分析:(1)过D作DE⊥AB,交AB于点E,理由角平分线性质得到DE=DC,利用HL得到Rt△ACD≌Rt△AED,由全等三角形的对应边相等,对应角相等,得到AC=AE,∠ACB=∠AED,由∠ACB=2∠B,利用等量代换及外角性质得到一对角相等,利用等角对等边得到BE=DE=DC,由AB=BE+AE,等量代换即可得证;
(2)AB=CD+AC,理由为:在AB上截取AG=AC,如图2所示,由角平分线定义得到一对角相等,再由![]() ,利用SAS得到△ADG≌△ADC,接下来同(1)即可得证;
,利用SAS得到△ADG≌△ADC,接下来同(1)即可得证;
(3)AB=CDAC,理由为:在AF上截取AG=AC,如图3所示,同(2)即可得证.
试题解析:(1)过D作DE⊥AB,交AB于点E,如图1所示,
∵AD为∠BAC的平分线,DC⊥AC,DE⊥AB,
∴DE=DC,
在Rt△ACD和Rt△AED中,
AD=AD,DE=DC,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ACB=∠AED,
∵∠ACB=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴BE=DE=DC,
则AB=BE+AE=CD+AC;
(2)AB=CD+AC,理由为:
在AB上截取AG=AC,如图2所示,
∵AD为∠BAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ADC中,
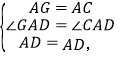
∴△ADG≌△ADC(SAS),
∴CD=DG,∠AGD=∠ACB,
∵∠ACB=2∠B,
∴∠AGD=2∠B,
又∵∠AGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BE=DG=DC,
则AB=BG+AG=CD+AC;
(3)AB=CDAC,理由为:
在AF上截取AG=AC,如图3所示,
∵AD为∠FAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ACD中,
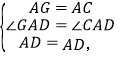
∴△ADG≌△ACD(SAS),
∴CD=GD,∠AGD=∠ACD,即∠ACB=∠FGD,
∵∠ACB=2∠B,
∴∠FGD=2∠B,
又∵∠FGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BG=DG=DC,
则AB=BGAG=CDAC.


【题目】政府计划投资14万亿元实施东进战略.为了解民对东进战略的关注情况,佳佳随机采访部分民,并对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 200 | 0.5 |
C.不关注 | 60 | n |
D.不知道 | 100 | 0.25 |
(1)采访总人数为__ __人,m=__ __,n=__ __;
(2)补全统计图;
(3)估计在30 000名民中高度关注东进战略的人数约为 人.