题目内容
【题目】已知,AB∥CD,AB,CD被直线l所截,点P是l上的一动点,连接PA,PC.
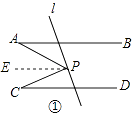
(1)如图①,当P在AB,CD之间时,求证:∠APC=∠A+∠C; 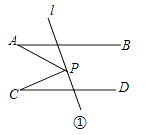
(2)如图②,当P在射线ME上时,探究∠A,∠C,∠APC的关系并证明; 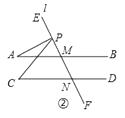
(3)如图③,当P在射线NF上时,直接写出∠A,∠C,∠APC三者之间关系. 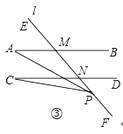
【答案】
(1)证明:如图①,过P点作,PE∥AB,则:∠A=∠APE,
∵AB∥CD,
∴PE∥CD
∴∠EPC=∠C.
又∵∠APC=∠APE+∠EPC,
∴∠APC=∠A+∠C
(2)解:如图②,
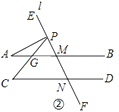
∵AB∥CD,
∴∠C=∠PGM.
∵∠PGM=∠A+∠APC,
∴∠C=∠A+∠APC
(3)解:如图③,
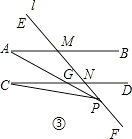
∵AB∥CD,
∴∠A=∠AGC.
∵∠AGC=∠C+∠APC,
∴∠A=∠C+∠APC.
【解析】(1)过P点作PE∥AB,则∠A=∠APE,再由AB∥CD得出PE∥CD,故∠EPC=∠C,利用等量代换即可得出结论;(2)先由平行线的性质得出∠C=∠PGM,再由三角形外角的性质即可得出结论;(3)根据AB∥CD得出∠A=∠AGC,再由三角形外角的性质即可得出结论.
【考点精析】通过灵活运用平行线的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.

练习册系列答案
相关题目