题目内容
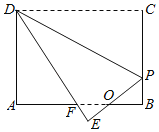
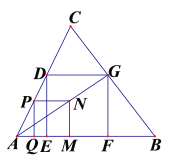
【题目】如图,正方形PQMN在△ABC内,点P在AC上,点Q、M在AB上,N在△ABC内,连接AN并延长交BC于G,过G点作GD∥AB交AC于D,过D、G分别作DE ⊥AB,GF⊥AB,垂足分别为E、F.
(1)求证:DG=GF;
(2)若AB=10,S△ABC=40,试求四边形DEFG的面积.
【答案】(1)见解析; (2)![]()
【解析】
(1)根据相似三角形的判定定理,证得△AMN∽△AFG,△APN∽△ADG,再根据相似三角形的对应边成比例可得![]() ,
,![]() ,根据正方形的性质判断PN=NM,进而求证DG=GF;
,根据正方形的性质判断PN=NM,进而求证DG=GF;
(2)如图,过点C作△ABC的高CI分别交DG、AB于点H、I,根据三角形的面积公式求出CI,由题(1)证得四边形DEFG是正方形,根据正方形的性质可得DE=EF=FG=DG,DE⊥AB,GF⊥AB,再设正方形DEFG的边长为x,根据三角形的面积公式求出S△CDG、S△ADE、S△BFG,根据正方形的面积公式可得:S正方形DEFG,由S△ABC=S△CDG+S△ADE+S△BFG+S正方形DEFG可列关于x的方程,解方程即可求得x,进而可求四边形DEFG的面积.
(1)∵DE⊥AB,GF⊥AB,GD∥AB
∴DE⊥DG,GF⊥DG
∴∠DEF=∠EFG=∠DGF=∠EDG=90°
∴四边形DGFE是矩形,
∵四边形PQME是正方形,
∴∠NMQ=90°,NM⊥AB,PN=NM
∴NM∥GF
∴△AMN∽△AFG
∴![]()
同理可得:![]()
∴![]()
∵PN=NM
∴GF=DG
(2)如图,过点C作△ABC的高CI分别交DG、AB于点H、I,
易知CI⊥AB,CH⊥DG
∵AB=10,S△ABC=40,
![]()
∴CI=8,
由(1)知:四边形DEFG是矩形,且GF=DG
∴四边形DEFG是正方形
∴DE=EF=GF=DG=HI,DE⊥AB,GF⊥AB,
设DE=EF=GF=DG=HI=x,
则CH=CI-HI=8-x,AE+BF=AB-EF=10-x,
∴S△CDG=![]() DG·CH=
DG·CH=![]() ,
,
S△ADE=![]() AE·DE=
AE·DE=![]() ,S△BFG=
,S△BFG=![]() BF·GF=
BF·GF=![]() ,
,
S正方形DEFG=![]() ,
,
∴S△ADE+S△BFG=![]() =
=![]() ,
,
∵S△CDG+S△ADE+S△BFG+S正方形DEFG=S△ABC=40,
∴![]() +
+![]() +
+![]() =40,
=40,
整理得:![]() ,
,
解得:![]() ,
,
∴S四边形DEFG =![]() =
=![]()

【题目】某品牌手机销售公司有营销员14人,销售部为制定营销人员月销售手机定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 165 | 80 | 50 | 40 |
人 数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)求这14位营销员该月销售该品牌手机的平均数、中位数和众数.
(2)销售部经理把每位营销员月销售量定为100台,你认为是否合理?为什么?