题目内容
【题目】如图，平面直角坐标系中，分别以点A(2，3)、点B(3，4)为圆心，以1、3为半径作⊙A、⊙B，M，N分别是⊙A、⊙B上的动点，P为x轴上的动点，则PM+PN的最小值为_____．
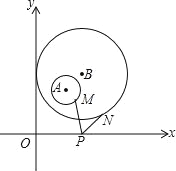
【答案】5
-4．
【解析】
试题作⊙A关于x轴的对称⊙A′，连接BA′分别交⊙A′和⊙B于M、N，交x轴于P，如图，根据两点之间线段最短得到此时PM+PN最小，再利用对称确定A′的坐标，接着利用两点间的距离公式计算出A′B的长，然后用A′B的长减去两个圆的半径即可得到MN的长，即得到+PN的最小值．
试题解析：作⊙A关于x轴的对称⊙A′，连接BA′分别交⊙A′和⊙B于M、N，交x轴于P，如图，
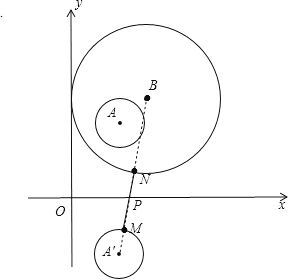
则此时PM+PN最小，
∵点A坐标（2，3），
∴点A′坐标（2，-3），
∵点B（3，4），
∴A′B=
，
∴MN=A′B-BN-A′M=5-3-1=5-4，
∴PM+PN的最小值为5-4．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】一个不透明的袋中装有2个黄球，1个红球和1个白球，除色外都相同．
(1)搅匀后，从袋中随机出一个球，恰好是黄球的概是_____？
(2)搅匀后，从中随机摸出两个球，求摸到一个红球和一个黄球的概率．
【题目】某中学为了了解“校园文明监督岗”的值围情况，对全校各班级进行了抽样调查，过程如下：
收集数据：从三个年级中随机抽取了20个班级，学校对各班的评分如下：
92 71 89 82 69 82 96 83 77 83
80 82 66 73 82 78 92 70 74 59
整理、描述数据：按如下分数段整理、描述这两组样本数据：
分数段 |
|
|
|
|
|
班级数 | 1 | 2 | a | 8 | b |
说明：成绩90分及以上为优秀，
分为良好，
分为合格，60分以下为不合格
分析数据：样本数据的平均数、中位数、众数、极差如下表，绘制扇形统计图：
平均数 | 中位数 | 众数 | 极差 |
79 | c | 82 | d |
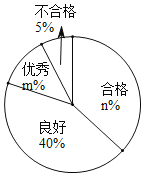
请根据以上信息解答下列问题：
填空：
______，
______，
______，
______．
若我校共120个班级，估计得分为优秀的班级有多少个？
为调动班级积极性，决定制定一个奖励标准分，凡到达或超过这个标准分的班级都将受到奖励
如果要使得半数左右的班级都能获奖，奖励标准分应定为多少分？并简述其理由
