Question

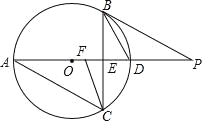
【题目】如图，已知△ABC内接于⊙O，直径AD⊥BC于E，点F是OE的中点，且BD∥CF．

(1)若BD＝3，求BC的长．

(2)若BD平分∠CBP，求证：ABBD＝BPAF．

Answer 1

【答案】(1)BC=2；(2)证明见解析.

【解析】

（1）由直径AD⊥BC，根据垂径定理得到E为BC中点，又BD与CF平行，得到两对内错角相等，从而利用“AAS”得到三角形BDE与三角形CFE全等，根据全等三角形的对应边相等得到DE=EF，设ED=EF=x，由已知F为OE中点，得到OE=2EF=2x，OD=OA=3x，则AD=6x，再由直径AB所对的圆周角为直角得到∠ABD=90°，又根据垂直定义得到∠AEB=90°，故两个角相等，再根据∠BED为公共角，利用两对对应角相等的两三角形相似得到△ABD∽△BED，由相似得比例列出关于x的方程，求出方程的解即可得到x的值，即可求出BD和DE，在直角三角形BDE中，利用勾股定理求出BE的长，进而求出BC的长；
（2）连接BF，根据AB为圆的直径，得到其所对的圆周角为直角，根据直角三角形两锐角互余得到∠BAD+∠ADB=90°又根据AD与BC垂直根据垂直定义得到一个直角，同理可得∠DBE+∠ADB=90°，根据同角的余角相等得到∠BAD=∠DBE，根据角平分线定义得到∠PBD=∠DBE，利用等量代换得到∠BAD=∠PBD，由（1）可知BE垂直平分FD，故BF=BD，根据“等边对等角”得到∠BFD=∠BDF，再根据等角的邻补角相等得到一对角相等，由两对对应角相等的两三角形相似，得到△ABF∽△BPD，由相似得比例变形后得证．

解：(1)∵直径AD⊥BC于E，

由垂径定理得：BE＝CE，

又∵BD∥CF，

∴∠ECF＝∠EBD，∠EFC＝∠EDB，

∴△BED≌△CEF，

∴DE＝EF，

设DE＝EF＝x，

又∵点F是OE的中点，

∴OE＝2EF＝2x，OD＝OA＝3x，AD＝6x，

∵AD是⊙O直径，

∴∠ABD＝90°，

又AD⊥BC，∴∠AEB＝90°，

∴∠ABD＝∠AEB，又∠BDE＝∠BDE，

∴△ABD∽△BED，

∴，即，

解得：x＝，

在直角三角形BDE中，

根据勾股定理得：BE＝，

则BC＝2BE＝2；

(2)连接BF，AB，

∵AD是⊙O直径，

∴∠ABD＝90°，

∴∠BAD+∠ADB＝90°

又AD⊥BC，∴∠AEB＝90°，

∴∠DBE+∠ADB＝90°，

∴∠BAD＝∠DBE，

又∵BD平分∠CBP，

∴∠PBD＝∠DBE，

∴∠BAD＝∠PBD，

由(1)可知：DE＝EF，且AD⊥BC，

∴BE是DF的垂直平分线，

∴BF＝BD，

∴∠BFD＝∠BDF，

∴∠AFB＝∠BDP，

∴△ABF∽△BPD，

∴，即ABBD＝BPAF．