��Ŀ����
����Ŀ������ijһ�����������¶��壺������ʵ��m�������Ա�����ֵΪmʱ���亯��ֵ���ک�m����Ʃ�mΪ��������ķ���ֵ���ں������ڷ���ֵʱ���ú����������ֵ����С����ֵ֮��n��Ϊ��������ķ�����룮�ر�أ�������ֻ��һ������ֵʱ���䷴�����nΪ�㣮
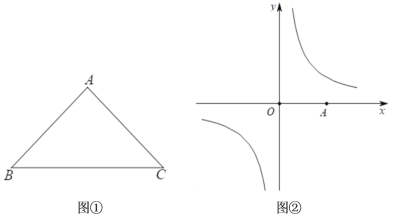
���磬ͼ�еĺ�����4����1��������ֵ���䷴�����n����5��
��1���ֱ��жϺ���y����x+1��y��![]() ��y��x2��û�з���ֵ������У�ֱ��д���䷴����룻
��y��x2��û�з���ֵ������У�ֱ��д���䷴����룻
��2�����ں���y��x2��b2x��
�����䷴�����Ϊ�㣬��b��ֵ��
������1��b��3�����䷴�����n��ȡֵ��Χ��
��3��������y�� ��ֱ��д����������ķ����������п���ֵ����д����Ӧm��ȡֵ��Χ��
��ֱ��д����������ķ����������п���ֵ����д����Ӧm��ȡֵ��Χ��

���𰸡���1��y��x2�з���ֵ�����������1����2����b����1����0��n��8����3����m��2��m�ܩ�2ʱ��n��2������2��m��2ʱ��n��4��
��������
(1)������Ŀ�е��¶�����Էֱ��������������Ƿ��з���ֵ���з���ֵ�Ŀ��������Ӧ�ķ�����룻
(2)������������������Ӧ��b��ֵ��
�����������b��ȡֵ��Χ���������Ӧ��n��ȡֵ��Χ��
(3)������Ŀ�еĺ�������ʽ��������Խ���⣮
(1)������ɵã�
����m����m+1ʱ���÷����⣬�ʺ���y����x+1û�з���ֵ��
����m��![]() ʱ��m����1����n��1��(��1)��2����y��
ʱ��m����1����n��1��(��1)��2����y��![]() �з���ֵ���������Ϊ2��
�з���ֵ���������Ϊ2��
����m��m2����m��0��m����1����n��0��(��1)��1����y��x2�з���ֵ�����������1��
(2)���m��m2��b2m��
��ã�m��0��m��b2��1��
���������Ϊ�㣬
��|b2��1��0|��0��
��ã�b����1��
���m��m2��b2m��
��ã�m��0��m��b2��1��
��n��|b2��1��0|��|b2��1|��
����1��b��3��
��0��n��8��
(3)��y��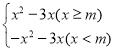 ��
��
����x��mʱ��
��m��m2��3m����m��0��m��2��
��n��2��0��2��
��m��2��m����2��
��x��mʱ��
��m����m2��3m��
��ã�m��0��m����4��
��n��0��(��4)��4��
����2��m��2��
���Ͽɵã���m��2��m����2ʱ��n��2��
����2��m��2ʱ��n��4��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ����ѧ��������ҵ������5��Ԫ��Ʒ��ר���꣬��֪��Ʒ����Ʒ�ɱ�Ϊÿ��aԪ���г����鷢����������y�����������ۼ�x��Ԫ/����֮�����һ�κ�����ϵ�����
���ۼ�x��Ԫ/���� | �� | 110 | 115 | 120 | 125 | 130 | �� |
������y������ | �� | 50 | 45 | 40 | 35 | 30 | �� |
���õ�ij������ۼ۶�Ϊ110Ԫ/��������3��Ա��������������֧ƽ�⣨����֧��=��Ʒ�ɱ�+Ա������+Ӧ֧���������ã�����֪Ա���Ĺ���Ϊÿ��ÿ��100Ԫ��ÿ�컹Ӧ֧����������Ϊ200Ԫ�����������ʿ��
��1������������y�����������ۼ�x��Ԫ/����֮��ĺ�����ϵʽ��
��2���õ�����2��Ա��������ÿ����װ�����ۼ۶�Ϊ����Ԫʱ���÷�װ��ÿ���ë�������ë�����T��������һ��Ʒ�ɱ�һԱ������һӦ֧���������ã�
��3���ڣ�2���������£���ÿ��ë����ȫ����������һ���Ի�������ʿ�ÿ��Ӧ�������֮��������֧����Ϣ����õ�������Ҫ�����죨ȡ���������ܻ��弯�ʿ