题目内容
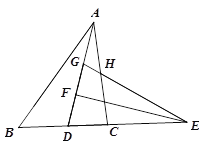
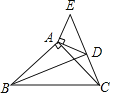
【题目】如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,则下列结论错误的是( )
A. △ABD≌△ACE B. ∠ACE+∠DBC=45°
C. BD⊥CE D. ∠BAE+∠CAD=200°
【答案】D
【解析】
根据SAS即可证明△ABD≌△ACE,再利用全等三角形的性质以及等腰直角三角形的性质即可一一判断.
∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
在△BAD和△CAE中,∵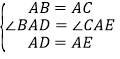 ,∴△BAD≌△CAE(SAS),∴BD=CE,故A正确;
,∴△BAD≌△CAE(SAS),∴BD=CE,故A正确;
∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°,∴∠ABD+∠DBC=45°.
∵△BAD≌△CAE,∴∠ABD=∠ACE,∴∠ACE+∠DBC=45°,故B正确.
∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°,∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,则BD⊥CE,故C正确.
∵∠BAC=∠DAE=90°,∴∠BAE+∠DAC=360°﹣90°﹣90°=180°,故D错误.
故选D.

 阅读快车系列答案
阅读快车系列答案【题目】2020年东京奥运会的比赛门票开始接受公众预订.下表为奥运会官方票务网站公布的几种球类比赛的门票的人民币价格,球迷小李用12000元做为预订下表中比赛项目门票的资金.
比赛项目 | 票价(元/场) |
男篮 | 1000 |
足球 | 800 |
乒乓球 | 500 |
(1)若全部资金用来预订男篮门票和乒乓球门票共15张,问男篮门票和乒乓球门票各订多少张?
(2)若在准备资金允许的范围内和总票数不变的前提下,这个球迷想预定上表中三种球类门票,其中足球门票与乒乓球门票数相同,且足球门票的费用不超过男篮门票的费用,问可以预订这三种球类门票各多少张?