题目内容
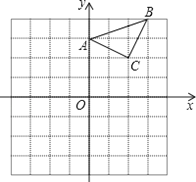
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是1个单位长度).
(1)画出△ABC关于x轴的轴对称图形,得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
【答案】(1)见解析,(2,-2);(2)(1,0),见解析;(3)10
【解析】
(1)直接利用平移的性质得出各对应点位置进而得出答案;
(2)利用位似图形的性质得出对应点位置进而得出答案;
(3)直接利用△A2B2C2所在矩形面积减去周围三角形面积进而得出答案.
(1)如图所示:△A1B1C1,即为所求,C1(2,-2);
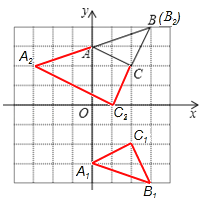
(2)如图所示:△A2B2C2,即为所求,C2(1,0);
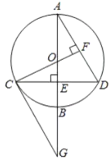
(3)△A2B2C2的面积是:4×6-![]() ×2×6-
×2×6-![]() ×2×4-
×2×4-![]() ×2×4=10.
×2×4=10.
故答案为:10.

练习册系列答案
相关题目