题目内容
【题目】已知x1,x2 是关于x的方程(x-2)(x-m)=(p-2)(p-m)的两个实数根.
(1)求x1,x2 的值;
(2)若x1,x2 是某直角三角形的两直角边的长,问当实数m,p满足什么条件时,此直角三角形的面积最大?并求出其最大值.
【答案】(1)x1 = p,x2 = m + 2-p;
(2)当![]() 且m>-2时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为
且m>-2时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为![]() (或
(或![]() ).
).
【解析】试题分析:(1)化简方程,用分解因式法求出两根;
(2)直角三角形的面积为![]() x1x2,利用根与系数的关系可以得到关于p的关系式,然后利用二次函数可以求出什么时候有最大值.
x1x2,利用根与系数的关系可以得到关于p的关系式,然后利用二次函数可以求出什么时候有最大值.
试题解析:(1) 原方程变为:x2-(m + 2)x + 2m = p2-(m + 2)p + 2m,
∴ x2-p2-(m + 2)x +(m + 2)p = 0,
(x-p)(x + p)-(m + 2)(x-p)= 0,
即 (x-p)(x + p-m-2)= 0,
∴ x1 = p, x2 = m + 2-p.
(2)∵ 直角三角形的面积为![]() x1x2=
x1x2=![]() p(m+2-p)
p(m+2-p)
= ![]()
=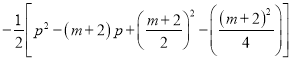
= ,
,
∴ 当![]() 且m>-2时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为
且m>-2时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为![]() (或
(或![]() ).
).

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】目前![]() 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?