��Ŀ����
����Ŀ����ͼ���㣺
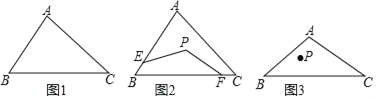
(1)��֪��ABC�����ó߹���ͼ1�С�ABC��ȷ��һ����P��ʹ�õ�P��AB��BC�ľ�����ȣ�������P����B�͵�C�ľ������(��д������������ͼ�ۼ�)��
(2)��ͼ2�������P��(1)�������ĵ㣬��E��F�ֱ��ڱ�AB��BC�ϣ���PE��PF��
������ABC��60�㣬���EPF�Ķ�����
����BE��2��BF��8��EP��5����BP�ij���
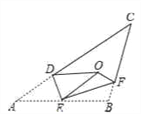
(3)��ͼ3�������P�ǡ�ABC��һ�㣬�ҵ�P����B�ľ�����7������ABC��45�㣬��ֱ���AB��BC������������M��N��ʹ�á�PMN���ܳ���С(��д������������ͼ�ۼ�)�����PMN����СֵΪ______.
���𰸡�(1)��������(2)�١�EPF��120�㣻��BP��![]() ��(3)7
��(3)7![]() .
.
��������
��1������ABC��ƽ����BM���߶�BC�Ĵ�ֱƽ����EF��ֱ��EF������BM�ڵ�P����P��Ϊ����
��2������Rt��PME��Rt��PNF��HL�����Ƴ���EPM=��FPN���Ƴ���EPF=��MPN�����ɽ�����⣻
����Rt��PMB��Rt��PNB��HL�����Ƴ�BM=BN����Rt��PME��Rt��PNF��HL�����Ƴ�EM=FN���Ƴ�BE+BF=BM-EM+BN+NF=2BN=10���Ƴ�BN=NM=5�������ù��ɶ������ɽ�����⣻
��3���ֱ�����P���ڱ�AB��BC�ĶԳƵ�E��F������EF���ֱ����AB��BC���ڵ�M��N������PM��PN�����߶�EF�ij��ȼ�Ϊ��PMN���ܳ�����Сֵ��
�⣺(1)��ͼ����P��Ϊ����
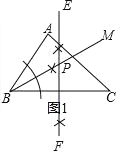
(2)������BP����PM��AB��M��PN��BC��N��
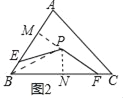
��BPƽ�֡�ABC��PM��AB��PN��BC��
��PM��PN��
��PE��PF����PME����PNF��90����
��Rt��PME��Rt��PNF(HL)��
���EPM����FPN��
���EPF����MPN��
�ߡ�MPN��360����90����90����60����120����
���EPF��120����
�ڡ�PB��PB��PM��PN����PMB����PFB��90��
��Rt��PMB��Rt��PNB(HL)��
��BM��BN��
��Rt��PME��Rt��PNF(HL)��
��EM��FN��
��BE+BF��BM��EM+BN+NF��2BN��10��
��BN��NM��5��
��BE��2��PE��5��
��EM��3��PM��![]() ��4��
��4��
��BP��![]() ��
��![]() ��
��
(3)�ֱ�����P���ڱ�AB��BC�ĶԳƵ�E��F������EF���ֱ����AB��BC���ڵ�M��N������PM��PN�����߶�EF�ij��ȼ�Ϊ��PMN���ܳ�����Сֵ��
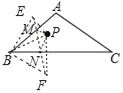
�ߵ�E���P����AB�Գƣ���F���P����BC�Գƣ�
���EBA����PBA����FBC����PBC��BE��BF��BP��7��
��EF��![]() BE��7
BE��7![]()
���PMN�ܳ�����СֵΪ7![]() ��
��
�ʴ�Ϊ7![]() ��
��