题目内容
【题目】顺次连结对角线相等的四边形的四边中点所得图形是( )
A.正方形
B.矩形
C.菱形
D.以上都不对
【答案】C
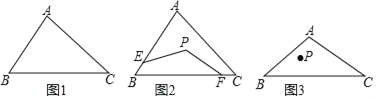
【解析】如图:已知四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,AC=BD,
连接AC、BD,
∵E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=![]() AC,GH=
AC,GH=![]() AC,GF=
AC,GF=![]() BD,EH=
BD,EH=![]() BD,
BD,
又∵AC=BD,
∴EF=GH=GF=EH,
∴四边形EFGH是菱形.
所以答案是:C.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
相关题目
【题目】某儿童游乐园门票价格规定如下表:
购票张数 | 1~50张 | 51~100张 | 100张以上 |
每张票的价格 | 13元 | 11元 | 9元 |
某校七年级(1)、(2)两个班共102人今年6.1儿童节去游该游乐园,其中(1)班人数较少,不足50人。经估算,如果两个班都以班为单位购票,则一共应付1218元。问:
(1)两个班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可以节省多少钱?