Question

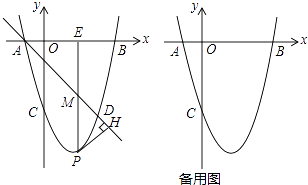
【题目】如图，在四边形ABCD中，∠B=90°，AB∥ED ,交BC于E，交 AC于F， DE = BC,.

（1） 求证：△FCD 是等腰三角形

（2） 若AB=3.5cm,求CD的长。

Answer 1

【答案】（1）详见解析；（2）CD=7cm.

【解析】

（1）首先根据平行线的性质得出∠DEC＝∠B＝90°，然后在△DCE中根据三角形内角和定理得出∠DCE的度数，从而得出∠DCF的度数．在△CDF中根据等角对等边证明出△FCD是等腰三角形；

（2）先证明△ACB≌△CDE，得出AC＝CD，再根据含30°角的直角三角形的性质求解即可．

（1）∵DE∥AB，∠B＝90°，∴∠DEC＝90°，∴∠DCE＝90°﹣∠CDE＝60°，∴∠DCF＝∠DCE﹣∠ACB＝30°，∴∠CDE＝∠DCF，∴DF＝CF，∴△FCD是等腰三角形；

（2）在△ACB和△CDE中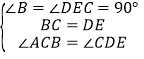，∵，∴△ACB≌△CDE，∴AC＝CD．

在Rt△ABC 中，∠B＝90°，∠ACB＝30°，AB＝3.5，∴AC＝2AB＝7，∴CD＝7．