��Ŀ����
����Ŀ������DEF�У�DE��DF����B��EF���ϣ��ҡ�EBD��60�㣬C������BD�ϵ�һ������(�����B�غϣ���BC��BE)��������BE�Ͻ�ȡBA��BC������AC��

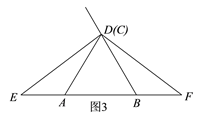
��1������C���߶�BD��ʱ��
������C���D�غϣ���������ⲹȫͼ1����ֱ��д���߶�AE��BF��������ϵΪ________��
����ͼ2������C�����D�غϣ���֤��AE��BF��CD��
��2������C���߶�BD���ӳ�����ʱ���õ�ʽ��ʾ�߶�AE��BF��CD֮���������ϵ������֤����
���𰸡���1����ͼ����������֤������������2��AE��BF��CD����AE��CD��BF.��
��������
����
��1������Ҫ��ȫͼ����ͼ3������֪������֤��ABD�ǵȱ������Σ���֤��DBE�ա�DAF���ɵ�BE=AF���Ӷ��ɵ�AE=BF������ͼ2����BE�Ͻ�ȡBG��BD������DG����֤��GBD����ABC���ǵȱ������Σ���֤��DGE�ա�DBF���ɵõ����������
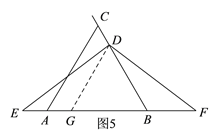
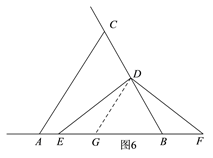
��2����ͼ5��ͼ6������C��BD�ӳ�����ʱ����ֵ�A���߶�BE�Ϻ��߶�BE���ӳ�������������������ۣ�����֪������֤��CAB�͡�DGB���ǵȱ������Σ��ɴ���DC=AG����֤��DGE�ա�DBF�ɵ�DG=BF�����ɵõ�DC��AE��BF���������ϵ.
��1������ȫͼ����ͼ3��ʾ��
��BA=BC����EBD=60�㣬
���ABDΪ�ȱ���������
���DAB=��DBA=60�㣬DB=DA��
��DE=DF��
���E=��F��
���DBE�ա�DAF��
��BE=AF��
��BE-AB=AF-AB����AE��BF��
����ͼ4����BE�Ͻ�ȡBG��BD������DG
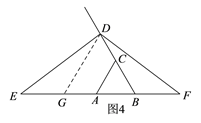
�ߡ�EBD��60�㣬BG��BD��
���GBD�ǵȱ������Σ�
ͬ������ABCҲ�ǵȱ������Σ�
��AG��CD.��DE��DF��
���E����F.
�֡ߡ�DGB����DBG��60�㣬
���DGE����DBF��120��.
���DGE�ա�DBF��
��GE��BF��
��AE��BF��CD.
��2����ͼ5��ͼ6������C��BD�ӳ�����ʱ����ֵ�A���߶�BE�Ϻ��߶�BE���ӳ�������������������ۣ�
������A���߶�BE��ʱ�����߶�BE�Ͻ�ȡBG=BD������DG��
�ߡ�DBE=60�㣬BA=BC��BG=BD��
���CBA����DBG���ǵȱ���������BA-BG=BC-BD��
���DGB=��DBG=60�㣬AG=CD��
���DGE=��DBF��
��DE=DF��
���E=��F��
���DGE�ա�DBF��
��GE=BF��
��AE=GE-AG=BF-CD��
��ͬ������ͼ6���ɵ�AE=CD-BF��
��������������C���߶�BD���ӳ�����ʱ��AE��BF��CD����AE��CD��BF��.

 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д�



