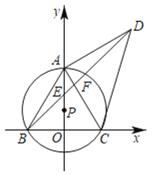
题目内容
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①若![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的值;
的值;
②![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
【答案】(1)![]() ;
;![]()
![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)将![]() 、
、![]() 的坐标代入
的坐标代入![]() 中,即可求解;
中,即可求解;
(2)确定直线![]() 的解析式为
的解析式为![]() ,根据点
,根据点![]() 、
、![]() 关于直线
关于直线![]() 对称,即可求解;
对称,即可求解;
(3)①![]() 与
与![]() 相似,则
相似,则![]() 或
或![]() ,即可求解;②分
,即可求解;②分![]() 、
、![]() 、
、![]() 三种情况,分别求解即可.
三种情况,分别求解即可.
解:(1))∵点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,![]() ,
,
∴![]() ,
,![]() ,
,
代入![]() 中,得:
中,得:![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为![]() ,
,
∴![]() 点坐标为
点坐标为![]() ;
;
(2)如图,连接BC,
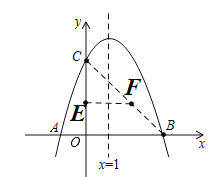
设直线![]() 的解析式为
的解析式为![]() ,
,
则有:![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
∵点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,
又![]() 到对称轴的距离为1,
到对称轴的距离为1,
∴![]() ,
,
∴![]() 点的横坐标为2,将
点的横坐标为2,将![]() 代入
代入![]() 中,
中,
得:![]() ,
,
∴![]() ;
;
(3)①如下图,
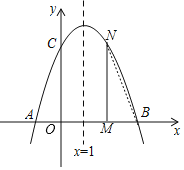
![]() ,
,![]() ,
,
![]() 与
与![]() 相似,则
相似,则![]() 或
或![]() ,
,
即:![]() 或
或![]() ,
,
解得:![]() 或
或![]() 或3或1(舍去
或3或1(舍去![]() 、
、![]() 、3),
、3),
故:![]() ;
;
②∵![]() ,
,![]() 轴,
轴,
∴![]() ,
,
∵![]() 为等腰三角形,
为等腰三角形,
∴分三种情况讨论,
第一种,当![]() 时,
时,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
第二种,当![]() 时,在
时,在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
第三种,当![]() 时,
时,
则点![]() 、
、![]() 重合,此时
重合,此时![]() ,
,
而![]() ,故不符合题意,
,故不符合题意,
综上述,当![]() 秒或
秒或![]() 秒时,
秒时,![]() 为等腰三角形.
为等腰三角形.

【题目】某市水果批发欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时,其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1) 如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.(总支出包含损耗、运费和装卸费用)
(2) 如果A市与B市之间的距离为S千米,你若是A市水果批发部门的经理,要想将这种水果运往B市销售,试分析以上两种运输工具中选择哪种运输方式比较合算呢?