题目内容
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 都在格点上。
都在格点上。
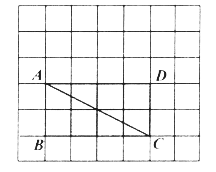
(Ⅰ)AC的长是_____________;
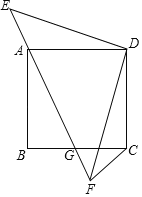
(Ⅱ)将四边形![]() 折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形
折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形![]() .请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点
.请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点![]() 的位置是如何找到的____________________.
的位置是如何找到的____________________.
【答案】![]() 如图所示,取格点
如图所示,取格点![]() 连接HO并延长分别交AD,BC于点F,E,连接BN,DM相交于点Q,则点E,F,为所求.
连接HO并延长分别交AD,BC于点F,E,连接BN,DM相交于点Q,则点E,F,为所求.

【解析】
(Ⅰ)根据勾股定理计算可得AC的长;
(Ⅱ)如图所示,取格点![]() 连接HO并延长分别交AD,BC于点F,E,连接BN,DM相交于点Q,则点E,F,为所求.
连接HO并延长分别交AD,BC于点F,E,连接BN,DM相交于点Q,则点E,F,为所求.
解:(Ⅰ)在Rt![]() 中,由勾股定理得:AC=
中,由勾股定理得:AC=![]() =
=![]() ,
,
(Ⅱ)如图所示

根据折叠的性质折痕EF垂直平分AC,取AC的中点格点O,根据AC是直角边长分别为2,4的直角三角形的斜边,要找过O与AC垂直的直线需找过点O且直角边长分别为2,4的直角三角形的斜边,取格点H,连接HO并延长分别交AD,BC于点F,E,则点E,F,为所求. 根据点D的对应点为Q,可知点D和点Q得关于OH对称,则OH垂直平分DQ,需QD//AC,QF=DF,取格点M使AM=2=CD,连接DM可得DM//AC;根据![]() ,可得DF=1.5,则PF=1.5,QF=1.5,则需 PQ⊥DQ,所以取点N连接BN即可
,可得DF=1.5,则PF=1.5,QF=1.5,则需 PQ⊥DQ,所以取点N连接BN即可

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目