Question

【题目】已知：在△EFG中，∠EFG＝90°，EF＝FG，且点E，F分别在矩形ABCD的边AB，AD上．

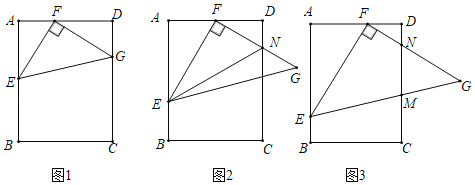
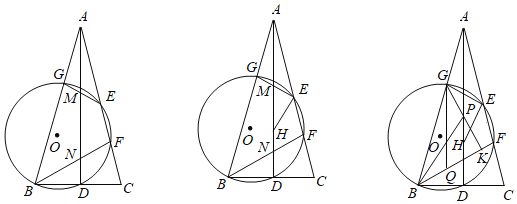
（1）如图1，当点G在CD上时，求证：△AEF≌△DFG；

（2）如图2，若F是AD的中点，FG与CD相交于点N，连接EN，求证：EN＝AE+DN；

（3）如图3，若AE＝AD，EG，FG分别交CD于点M，N，求证：MG2＝MNMD.

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析.

【解析】

（1）先用同角的余角相等，判断出∠AEF＝∠DFG，即可得出结论；

（2）先判断出△AHF≌△DNF，得出AH＝DN，FH＝FN，进而判断出EH＝EN，即可得出结论；

（3）先判断出AF＝PG，PF＝AE，进而判断出PG＝PD，得出∠MDG＝45°，进而得出∠FGE＝∠GDM，判断出△MGN∽△MDG，即可得出结论．

（1）∵四边形ABCD是矩形，

∴∠A＝∠D＝90°，

∴∠AEF+∠AFE＝90°，

∵∠EFG＝90°，

∴∠AFE+∠DFG＝90°，

∴∠AEF＝∠DFG，

∵EF＝FG，

∴△AEF≌△DFG（AAS）；

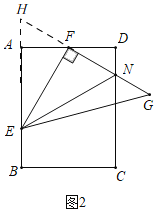
（2）如图2，，

延长NF，EA相交于H，

∴∠AFH＝∠DFN，

由（1）知，∠EAF＝∠D＝90°，

∴∠HAF＝∠D＝90°，

∵点F是AD的中点，

∴AF＝DF，

∴△AHF≌△DNF（ASA），

∴AH＝DN，FH＝FN，

∵∠EFN＝90°，

∴EH＝EN，

∵EH＝AE+AH＝AE+DN，

∴EN＝AE+DN；

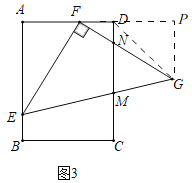
（3）如图3，

过点G作GP⊥AD交AD的延长线于P，

∴∠P＝90°，

同（1）的方法得，△AEF≌△PFG（AAS），

∴AF＝PG，PF＝AE，

∵AE＝AD，

∴PF＝AD，

∴AF＝PD，

∴PG＝PD，

∵∠P＝90°，

∴∠PDG＝45°，

∴∠MDG＝45°，

在Rt△EFG中，EF＝FG，

∴∠FGE＝45°，

∴∠FGE＝∠GDM，

∵∠GMN＝∠DMG，

∴△MGN∽△MDG，

∴，

MG2＝MNMD．