Question

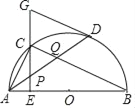
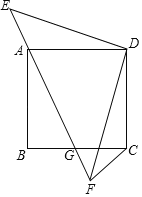
【题目】如图示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BC相交于点G，连接CF．

①求证：△DAE≌△DCF；

②求证：△ABG∽△CFG．

Answer 1

【答案】①.证明见解析；②证明见解析.

【解析】

试题①由正方形ABCD与等腰直角三角形DEF，得到两对边相等，一对直角相等，利用SAS即可得证；②由第一问的全等三角形的对应角相等，根据等量代换得到∠BAG=∠BCF，再由对顶角相等，利用两对角相等的三角形相似即可得证．

试题解析：①∵正方形ABCD，等腰直角三角形EDF，∴∠ADC=∠EDF=90°，AD=CD，DE=DF，

∴∠ADE+∠ADF=∠ADF+∠CDF，∴∠ADE=∠CDF，

在△ADE和△CDF中，，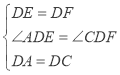

∴△ADE≌△CDF；

②延长BA到M，交ED于点M，

∵△ADE≌△CDF，∴∠EAD=∠FCD，即∠EAM+∠MAD=∠BCD+∠BCF，

∵∠MAD=∠BCD=90°，∴∠EAM=∠BCF，∵∠EAM=∠BAG，∴∠BAG=∠BCF，

∵∠AGB=∠CGF，∴△ABG∽△CFG．