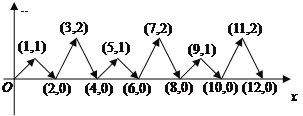题目内容
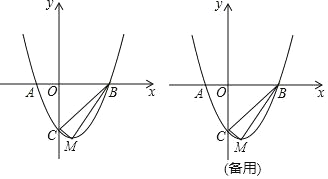
【题目】已知:如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于点C,该抛物线的顶点为M.
(1)求点A、B、C的坐标.
(2)求直线BM的函数解析式.
(3)试说明:∠CBM+∠CMB=90°.
(4)在抛物线上是否存在点P,使直线CP把△BCM分成面积相等的两部分?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)点A(﹣1,0),点B(3,0),点C坐标为(0,﹣3);(2)y=2x﹣6;(3)证明见解析;(4)点P坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)根据题意可以直接可求点A、B、C的坐标;
(2)用待定系数法可求解析式;
(3)根据两点距离公式可求BM,BC,CM的长度,根据勾股定理的逆定理可得∠BCM=90°,即可证:∠CBM+∠CMB=90°;
(4)根据题意可求线段BM中点坐标,即可求直线CP解析式,且点P在抛物线上,可列方程,即可求点P坐标.
(1)∵抛物线y=x2﹣2x﹣3与x轴交于A、B两点,∴0=x2﹣2x﹣3,∴x1=3,x2=﹣1,∴点A(﹣1,0),点B(3,0).
∵抛物线y=x2﹣2x﹣3与y轴交于点C,∴当x=0时,y=﹣3,∴点C坐标为(0,﹣3);
(2)∵抛物线y=x2﹣2x﹣3=(x﹣1)2﹣4,∴点M(1,﹣4).
设直线BM的解析式:y=kx+b过点B(3,0),M(1,﹣4),∴![]()
解得:k=2,b=﹣6.
∴直线BM的解析式:y=2x﹣6.
(3)∵点M(1,﹣4),点B(3,0),点C(0,﹣3),∴BC=![]() =3
=3![]()
BM=![]() =2
=2![]()
CM=![]() =
=![]()
∵BC2+CM2=20,BM2=20,∴BC2+CM2=BM2,∴∠BCM=90°,∴∠CBM+∠CMB=90°.
(4)如图:设直线CP与BM的交点为F.
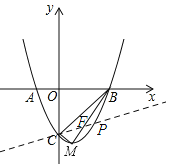
∵直线CP把△BCM分成面积相等的两部分,∴S△CMF=S△BCF.
∵△CMF和△BCF是等高的两个三角形,∴FM=BF,即点F是BM的中点.
∵点B(3,0),点M(1,﹣4),∴点F坐标为(2,﹣2).
设直线CP的解析式为y=mx+n,∴![]()
解得:m=![]() ,n=﹣3
,n=﹣3
∴直线CP解析式y=![]() x﹣3.
x﹣3.
∵点P是直线CP与抛物线y=x2﹣2x﹣3的交点,∴![]() x﹣3=x2﹣2x﹣3
x﹣3=x2﹣2x﹣3
解得:x1=0(不合题意舍去),x2=![]() .
.
当x=![]() 时,y=
时,y=![]() ﹣2×
﹣2×![]() =﹣
=﹣![]() ,∴点P坐标为(
,∴点P坐标为(![]() ,﹣
,﹣![]() ).
).

 阅读快车系列答案
阅读快车系列答案