题目内容
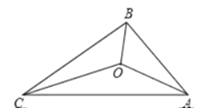
【题目】如图,在△ ABC中,AB=AC,点D在线段BC上,AD=BD,△ ADC是等腰三角形,求△ABC三个内角的度数。
【答案】∠BAC=108°,∠B=∠C=36°或∠BAC=90°,∠B=∠C=45°
【解析】
△ ADC是等腰三角形,分类讨论:分AC=DC或AD=DC两种情况;当AC=DC时,利用等腰三角形的等边对等角,设∠B![]() ,利用三角形的外角的性质求得∠ADC=∠B+∠BAD
,利用三角形的外角的性质求得∠ADC=∠B+∠BAD![]() ,然后利用三角形的内角和构建方程求解即可;当AD=DC时,利用等腰三角形的等边对等角结合三角形内角和定理即可求得答案.
,然后利用三角形的内角和构建方程求解即可;当AD=DC时,利用等腰三角形的等边对等角结合三角形内角和定理即可求得答案.
∵ △ ADC是等腰三角形
当AC=DC时
∴ ∠DAC=∠ADC
又∵ AB=AC,AD=BD
∴ ∠B=∠C=∠BAD
设∠B![]() ,则∠ADC= ∠B+∠BAD
,则∠ADC= ∠B+∠BAD![]()
∴∠DAC=∠ADC![]() ,∠BAC=∠DAC+∠BAD
,∠BAC=∠DAC+∠BAD![]()
于是在△ ABC中,有 ∠B+∠C+∠BAC![]() 180°
180°
解得![]()
所以,在△ ABC中,∠BAC=108°,∠B=∠C=36°
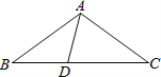
当AD=DC时,如下图:
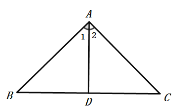
∵AD=DC,
∴∠2=∠C,
∵AB=AC,
∴∠B=∠C
∵AD=BD,
∴∠B=∠1,
∴∠B=∠C=∠1=∠2,
∵∠B+∠C+∠1+∠2=180![]() ,
,
∴∠B+∠C=45![]() ,∠1+∠2=90°,
,∠1+∠2=90°,
∠BAC=∠1+∠2=90°,
所以,在△ ABC中,∠BAC=90°,∠B=∠C=45°

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目