题目内容
【题目】在![]() 中,
中,![]() ,翻折
,翻折![]() ,使点
,使点![]() 落在斜边
落在斜边![]() 上某一点
上某一点![]() 处,折痕为
处,折痕为![]() (点
(点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上)
上)
![]() 当
当![]() 时,若
时,若![]() 与
与![]() 相似(如图
相似(如图![]() ),求
),求![]() 的长;
的长;
![]() 当点
当点![]() 是
是![]() 的中点时(如图
的中点时(如图![]() ),
),![]() 与
与![]() 相似吗?请说明理由.
相似吗?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析
,理由见解析
【解析】
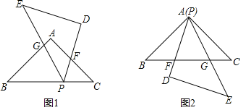
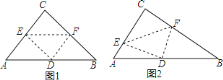
(1)如图1,连接CD,由已知条件得到△ABC是等腰直角三角形由于△CEF与△ABC相似,于是得到△CEF也是等腰直角三角形求得∠CEF=∠A=45°,于是得到EF∥AB,由轴对称的性质等等EF⊥CD,求出CD⊥AB,根据直角三角形的性质即可得到结论;
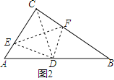
(2)如图2,连接CD,与EF交于点Q,根据直角三角形的性质得到CD=DB=![]() AB,于是得到∠DCB=∠B,由轴对称的性质得到∠CQF=∠DQF=90°,推出∠DCB+∠CFE=90°,由于∠B+∠A=90°,于是得到∠CFE=∠A,即可得到结论.
AB,于是得到∠DCB=∠B,由轴对称的性质得到∠CQF=∠DQF=90°,推出∠DCB+∠CFE=90°,由于∠B+∠A=90°,于是得到∠CFE=∠A,即可得到结论.
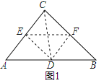
![]() 如图
如图![]() ,连接
,连接![]() ,
,
∵![]() ,
,
∴![]() 是等腰直角三角形
是等腰直角三角形
又∵![]() 与
与![]() 相似,
相似,
∴![]() 也是等腰直角三角形
也是等腰直角三角形
∴![]() ,
,
∴![]() ,
,
由轴对称的性质知:![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴点![]() 是
是![]() 的中点,
的中点,
∴![]() ;
;
![]() 当点
当点![]() 是
是![]() 的中点时,
的中点时,![]() 与
与![]() 相似,
相似,
理由如下:如图![]() ,连接
,连接![]() ,与
,与![]() 交于点
交于点![]() ,
,
∵![]() 是
是![]() 的中线,
的中线,
∴![]() ,
,
∴![]() ,
,
由轴对称的性质可知,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】.鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组
“鞋码”与鞋长换算的对应数值:[注:“鞋码”是表示鞋子大小的一种号码]
鞋长(cm) | 16 | 19 | 21 | 24 |
鞋码(号) | 22 | 28 | 32 | 38 |
(1)设鞋长为x,“鞋码”为y,试判断点(x,y)在你学过的哪种函数的图象上?
(2)求x、y之间的函数关系式;(3)如果某人穿44号“鞋码”的鞋,那么他的鞋长是多少?