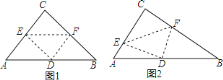
题目内容
【题目】如图,![]() 、
、![]() 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,![]() .
.
![]() 若将
若将![]() 的顶点
的顶点![]() 放在
放在![]() 上(如图
上(如图![]() ),
),![]() 、
、![]() 分别与
分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() .求证:
.求证:![]() ;
;
![]() 若使
若使![]() 的顶点
的顶点![]() 与顶点
与顶点![]() 重合(如图
重合(如图![]() ),
),![]() 、
、![]() 与
与![]() 相交于点
相交于点![]() 、
、![]() .试问
.试问![]() 与
与![]() 还相似吗?为什么?
还相似吗?为什么?
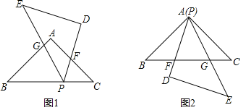
【答案】(1)见解析;(2)![]() 与
与![]() 相似.理由见解析
相似.理由见解析
【解析】
(1)如图1,先根据等腰直角三角形的性质得∠B=∠C=∠DPE=45°,再利用平角定义得到∠BPG+∠CPF=135°,利用三角形内角和定理得到∠BPG+∠BGP=135°,根据等量代换得∠BGP=∠CPF,加上∠B=∠C,于是根据有两组角对应相等的两个三角形相似即可得到结论;
(2)如图2,由于∠B=∠C=∠DPE=45°,利用三角形外角性质得∠BGP=∠C+∠CPG=45°+∠CAG,而∠CPF=45°+∠CAG,所以∠AGP=∠CPF,加上∠B=∠C,于是可判断△PBG∽△FCP.
![]() 证明:如图
证明:如图![]() ,
,

∵![]() 、
、![]() 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
![]() 解:
解:![]() 与
与![]() 相似.理由如下:
相似.理由如下:
如图![]() ,∵
,∵![]() 、
、![]() 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目