题目内容
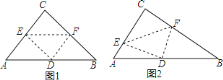
【题目】如图,在Rt△ABC中,∠BCA=90°,∠DCA=30°,AC=![]() ,AD=
,AD=![]() ,则BC的长为__.
,则BC的长为__.

【答案】5.
【解析】
作辅助线,构建直角三角形,先根据直角三角形30度角的性质和勾股定理得:AE=![]() ,CE=
,CE=![]() ,及ED的长,可得CD的长,证明△BFD∽△BCA,列比例式可得BC的长.
,及ED的长,可得CD的长,证明△BFD∽△BCA,列比例式可得BC的长.
过A作AE⊥CD于E,过D作DF⊥BC于F,
Rt△AEC中,∠ACD=30°,AC=![]() ,
,
∴AE=![]() ,CE=
,CE=![]() ,
,
Rt△AED中,ED=![]() =
=![]() =
=![]() ,
,
∴CD=CE+DE=![]() +
+![]() =
=![]() ,
,
∵DF⊥BC,AC⊥BC,
∴DF∥AC,
∴∠FDC=∠ACD=30°,
∴CF=![]() CD=
CD=![]() ×
×![]() =
=![]() ,
,
∴DF=![]()
![]() ,
,
∵DF∥AC,
∴△BFD∽△BCA,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BF=![]() ,
,
∴BC=![]() +
+![]() =5,
=5,
故答案为:5.

练习册系列答案
相关题目