题目内容
【题目】我们知道三角形任意两条中线的交点是三角形的重心．重心有如下性质：重心到顶点的距离是重心到对边中点距离的2倍．请利用该性质解决问题
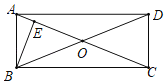
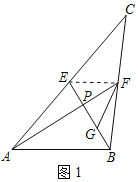
（1）如图1，在△ABC中，AF、BE是中线，AF⊥BE于P．若BP＝2，∠FAB＝30°，则EP＝ ，FP＝ ；
（2）如图1，在△ABC中，BC＝a，AC＝b，AB＝c，AF、BE是中线，AF⊥BE于P．猜想a2、b2、c2三者之间的关系并证明；
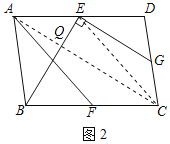
（3）如图2，在ABCD中，点E、F、G分别是AD、BC、CD的中点，BE⊥BG，AB＝3，AD＝2
，求AF的长．
【答案】（1）1，
；（2）a2+b2＝5c2，理由见解析；（3）AF＝4
【解析】
（1）由三角形的重心定理得出BP＝2EP＝2，AP＝2FP，得出EP＝1，由直角三角形的性质得出AP＝BP＝2，即可得出FP＝
AP＝；
（2）设PF＝m，PE＝n，由 
，得到AP＝2m，PB＝2n，再由勾股定理即可得出结论；
（3）连接AC、EC，由平行四边形的性质得出AD＝BC，AD∥BC，证明四边形AFCE是平行四边形，得出AF＝CE，由平行线得出△AEQ∽△CBQ，得出
，设AQ＝a，EQ＝b，则CQ＝2a，BQ＝2b，证明EG是△ACD的中位线，由三角形中位线定理得出EG∥AC，得出BE⊥AC，由勾股定理得得出方程，求出a2＝
，得出BQ2＝4b2＝
，b2＝
，在Rt△EQC中，由勾股定理求出CE，即可得出AF的长．
解：（1）∵在△ABC中，AF、BE是中线，
∴BP＝2EP＝2，AP＝2FP，
∴EP＝1，
∵AF⊥BE，∠FAB＝30°，
∴AB=2BP=4，
∴AP＝
，
∴FP＝AP＝；
故答案为：1，；
（2）a2+b2＝5c2；理由如下：
连接EF，如图1所示：
∵AF，BE是△ABC的中线，
∴EF是△ABC的中位线，
∴EF∥AB，且EF＝AB＝c，
∴，
设PF＝m，PE＝n，
∴AP＝2m，PB＝2n，
在Rt△APB中，（2m）2+（2n）2＝c2，即4m2+4n2＝c2，
在Rt△APE中，（2m）2+n2＝（b）2，即4m2+n2＝
b2，
在Rt△FPB中，m2+（2n）2＝（a）2，即m2+4n2＝a2，
∴5m2+5n2＝（a2+b2）＝
c2，
∴a2+b2＝5c2；
（3）连接AC、EC，如图2所示：
∵四边形ABCD是平行四边形，
∴AD＝BC，AD∥BC，
∵点E，F分别是AD，BC，CD的中点，
∴AE＝CE，
∴四边形AFCE是平行四边形，
∴AF＝CE，
∵AD∥BC，
∴△AEQ∽△CBQ，
∴，
设AQ＝a，EQ＝b，则CQ＝2a，BQ＝2b，
∵点E，G分别是AD，CD的中点，
∴EG是△ACD的中位线，
∴EG∥AC，
∵BE⊥EG，
∴BE⊥AC，
由勾股定理得：AB2﹣AQ2＝BC2﹣CQ2，
即9﹣a2＝（2
）2﹣4a2，
∴3a2＝11，
∴a2＝，
∴BQ2＝4b2＝（2）2﹣4×＝，
∴b2＝×＝，
在Rt△EQC中，CE2＝EQ2+CQ2＝b2+4a2＝16，
∴CE＝4，
∴AF＝4．
