题目内容
【题目】已知三角形的一锐角α(45°<α<90°)的正弦和余弦分别是方程(m+5)x2﹣(2m﹣5)x+12=0的两根,求:
(1)m的值;
(2)α的正弦值和余弦值.
【答案】(1)20;(2)sinα=![]() ,cosα=
,cosα=![]()
【解析】
(1)设一个直角三角形的两个锐角为∠A、∠B,且∠A+∠B=90°,利用正弦三角公式及完全平方公式得![]() ﹣2sinAsinB=1,列一元二次方程求解即可;
﹣2sinAsinB=1,列一元二次方程求解即可;
(2) 当m=20时,方程转化为(5x﹣3)(5x﹣4)=0,求解即可得到正弦值和余弦值,且注意α为锐角.
解:(1)设一个直角三角形的两个锐角为∠A、∠B(∠A+∠B=90°),
∴sinB=cosA,
根据题意,得:sinA+sinB=![]() ,sinAsinB=
,sinAsinB=![]() ,
,
∵![]() ,
,
∴![]() ﹣2sinAsinB=1,
﹣2sinAsinB=1,
∴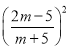 ﹣2×
﹣2×![]() =1,
=1,
解得![]() =20,
=20,![]() =﹣2,
=﹣2,
检验:把![]() =20代入检验是原方程的根,把
=20代入检验是原方程的根,把![]() =﹣2代入检验是原方程的根,
=﹣2代入检验是原方程的根,
∵sinA+sinB=![]() >0,sinAsinB=
>0,sinAsinB=![]() <1,
<1,
∴m=20;
(2)当m=20时,方程转化为(5x﹣3)(5x﹣4)=0,
解得![]() ,
,
∵45°<α<90°,
∴sinα>cosα,
∴sinα=![]() ,cosα=
,cosα=![]() .
.

练习册系列答案
相关题目