题目内容
如图4,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cosB=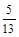 ,BC=26.
,BC=26.
求:

小题1:cos∠DAC的值;
小题2:线段AD的长
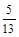 ,BC=26.
,BC=26.求:

小题1:cos∠DAC的值;
小题2:线段AD的长
小题1:
小题2:13
(1)由cosB=和BC=26,可求得,AB=10
可证得:∠ACB=∠ACD=∠DAC,由勾股定理可求得AC=24,
∴cos∠DAC=cos∠ACB=.
(2)取AC中点E,连接DE,AE=12,cos∠DAC=.
由等腰△ADC三线合一得DE⊥AC,∴Rt△AED中AD="AE/cos∠DAC=13."
可证得:∠ACB=∠ACD=∠DAC,由勾股定理可求得AC=24,
∴cos∠DAC=cos∠ACB=.
(2)取AC中点E,连接DE,AE=12,cos∠DAC=.
由等腰△ADC三线合一得DE⊥AC,∴Rt△AED中AD="AE/cos∠DAC=13."

练习册系列答案
相关题目
 △ADC除外);
△ADC除外);




 对角线
对角线 、
、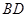 相交于点
相交于点 ,若
,若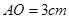 ,
, ,则菱形
,则菱形 .
.