题目内容
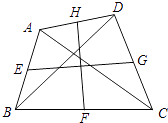
【题目】如图，用四条线段首尾相接连成一个框架，其中AB=12，BC=14，CD=18，DA=24，则A、B、C、D任意两点之间的最长距离为（ ） 
A.24cm
B.26cm
C.32cm
D.36cm
【答案】C
【解析】解：已知AB=12，BC=14，CD=18，DA=24； ①选12+14、18、24作为三角形，则三边长26、18、24；26﹣24＜18＜26+24，能构成三角形，此时两个端点间的最长距离为26；
②选12、14+18、24作为三角形，则三边长为12、32、24；32﹣24＜12＜32+24，能构成三角形，此时两个端点间的最大距离为32；
③选12、14、18+24作为三角形，则三边长为12、14、42；12＜42﹣14，不能构成三角形．
故选：C．
【考点精析】认真审题，首先需要了解三角形三边关系(三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边)．
练习册系列答案
相关题目
