Question

【题目】如图，在四边形ABCD中，AC=BD=6，E、F、G、H分别是AB、BC、CD、DA的中点，则EG2+FH2= ．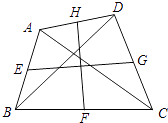

Answer 1

【答案】36
【解析】解：如右图，连接EF，FG，GH，EH， ∵E、H分别是AB、DA的中点，
∴EH是△ABD的中位线，
∴EH= BD=3，
同理可得EF，FG，GH分别是△ABC，△BCD，△ACD的中位线，
∴EF=GH= AC=3，FG= BD=3，
∴EH=EF=GH=FG=3，
∴四边形EFGH为菱形，
∴EG⊥HF，且垂足为O，
∴EG=2OE，FH=2OH，
在Rt△OEH中，根据勾股定理得：OE2+OH2=EH2=9，
等式两边同时乘以4得：4OE2+4OH2=9×4=36，
∴（2OE）2+（2OH）2=36，
即EG2+FH2=36．
所以答案是：36．

【考点精析】通过灵活运用勾股定理的概念和三角形中位线定理，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半即可以解答此题．