题目内容
已知:如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC与点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F。下列结论:①CD2=CE·CB;②4EF2=ED·EA;③∠OCB=∠EAB;④DF=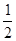 CD.其中正确的有 (填序号)
CD.其中正确的有 (填序号)
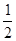 CD.其中正确的有 (填序号)
CD.其中正确的有 (填序号)
①、②、④
试题分析:先连接BD,利用相似三角形的判定以及切线的性质定理得出DF=FB,进而分别得出△CDE∽△CBD以及△CDF∽△CBO,再根据相似三角形的性质分别分析即可得出答案.:
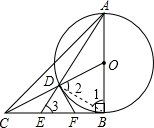 解:①连接BD,
解:①连接BD,∵AB为直径,
∴∠ADB=90°,
∴∠DBE+∠3=90°,
∵∠ABC=90°,
∴∠1+∠DBE=90°,
∴∠1=∠3,
又∵DO=BO,
∴∠1=∠2,
∴∠2=∠3,
∴∠CDB=∠CED,
∵∠DCB=∠ECD,
∴△CDE∽△CBD,
∴CD2=CE•CB,故①CD2=CE•CB正确;
②∵过D作⊙O的切线交BC于点F,
∴FD是⊙O的切线,
∵∠ABC=90°,
∴CB是⊙O的切线,
∴FB=DF,

∴∠FDB=∠FBD,
∴∠1=∠FDE,
∴∠FDE=∠3,
∴DF=EF,
∴EF=FB,
∴EB=2EF,
∵在Rt△ABE中,BD⊥AE,
∴EB2=ED•EA,
∴4EF2=ED•EA,故②4EF2=ED•EA正确;
③∵AO=DO,
∴∠OAD=∠ADO,
假设③∠OCB=∠EAB成立,
则∠OCB=0.5∠COB,
∴∠OCB=30°,
而
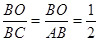 ,与tan30°=
,与tan30°=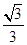 矛盾,
矛盾,故③∠OCB=∠EAB不成立,故此选项错误;
④∵∠CDF=∠CBO=90°,
∠DCF=∠OCB,
∴△CDF∽△CBO,
∴
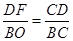 ,
,∴
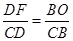 ,
,∵AB=BC,
∴DF=0.5CD;故④DF=0.5CD正确.
综上正确的有①、②、④.
故答案为:①②④.
点评:此题主要考查了圆的切线性质与判定、圆周角定理性质及三角形相似的判定等知识,熟练根据相似三角形的性质得出对应边之间关系是解题关键.

练习册系列答案
相关题目

 在同一条直线上,则阴影部分的面积是 .
在同一条直线上,则阴影部分的面积是 .




 ,
, ,则
,则 的长度是 .
的长度是 .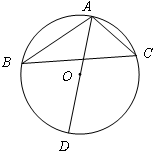

 ,AK=
,AK= ,求FG的长.
,求FG的长. 上,若OA=1,∠1=∠2,则扇形OEF的面积为 【 】
上,若OA=1,∠1=∠2,则扇形OEF的面积为 【 】
 B.
B. C.
C. D.
D.