题目内容
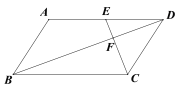
【题目】如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF =3,则S□ABCD =_______.
【答案】36
【解析】
由已知易得DE∥BC,DE:BC=1:2,由此可得△DEF∽△BCF,从而可得S△DEF:S△BCF=1:4,EF:CF=1:2,这样即可由S△DEF=3解得S△BCF=12,S△DCF=6,从而可得S△BCD=18,由此即可得到平行四边形ABCD的面积=36.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴DE:BC=EF:CF,
∵点E是AD边的中点,
∴DE:BC=1:2,
∴S△DEF:S△BCF=1:4,EF:CF=1:2,
∵S△DEF=3,
∴S△BCF=12,S△DCF=6,
∴S△BCD=12+6=18,
∴S平行四边形ABCD=2S△BCD=18×2=36.
故答案为:36.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目