题目内容
 (2013•永春县质检)如图,抛物线y=-x2+x+c与x轴交于A,B两点,与y轴交于点C,且点B的坐标为B(-2,0).
(2013•永春县质检)如图,抛物线y=-x2+x+c与x轴交于A,B两点,与y轴交于点C,且点B的坐标为B(-2,0).(1)求抛物线解析式;
(2)点P在抛物线上,且点P的横坐标为x(-2<x<0),设△PBC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点M(m,n)是直线AC上的动点.设m=2-a,如果在两个实数m与n之间(不包括m和n)有且只有一个整数,求实数a的取值范围.
分析:(1)把点B的坐标代入抛物线解析式,列出关于c的方程,通过解方程可以求得c的值;
(2)连接BC,过点P作PF∥y轴,交BC与点F.点P的横坐标为x,表示出F(x,3x+6),P(x,-x2+x+6),最后表示出PF的长,从而表示出S关于x的函数关系,然后求二次函数的最值即可.
(3)点M(m,n)是直线AC上的动点,由一次函数解析式可知,设m=2-a,则M(2-a,2a+2),依题意m≠n,a≠0.根据a>0和a<0两种情况,分别求实数a的取值范围.
(2)连接BC,过点P作PF∥y轴,交BC与点F.点P的横坐标为x,表示出F(x,3x+6),P(x,-x2+x+6),最后表示出PF的长,从而表示出S关于x的函数关系,然后求二次函数的最值即可.
(3)点M(m,n)是直线AC上的动点,由一次函数解析式可知,设m=2-a,则M(2-a,2a+2),依题意m≠n,a≠0.根据a>0和a<0两种情况,分别求实数a的取值范围.
解答: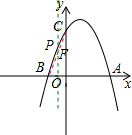 解:(1)如图,∵抛物线y=-x2+x+c与x轴交于A,B两点,点B的坐标为B(-2,0).
解:(1)如图,∵抛物线y=-x2+x+c与x轴交于A,B两点,点B的坐标为B(-2,0).
所以,-(-2)2+(-2)+c=0,即-6+c=0,
解得,c=6.
则该抛物线解析式是y=-x2+x+6;
(2)由(1)知,该抛物线解析式是y=-x2+x+6.
易求C(0,6).
设直线BC的解析式为y=k1x+6(k1≠0),则-2k1+6=0,
解得k1=3,
∴直线BC的解析式为y=3x+6.
∵点P的横坐标为x(-2<x<0),
∴F(x,3x+6),P(x,-x2+x+6),
∴PF=-x2+x+6-(3x+6)
=-x2-2x.
∴S=S△BPF+S△PCF,
=
|PF|•|OB|=-x2-2x=-(x+1)2+1,
∵-2<x<0,
∴当x=-1时,S最大=1.
综上所述,S与x之间的函数关系式是S=-x2-2x[或S=-(x+1)2+1],S的最大值是1;
(3)由(1)知,该抛物线解析式是y=-x2+x+6.则A(3,0).易求C(0,6).
设直线AC的解析式为y=k2x+6(k1≠0),则3k2+6=0,
解得k2=-2,
∴直线AC的解析式为y=-2x+6.
由已知M(2-a,2a+2),易知,m≠n,2-a≠2a+2,则a≠0.
若a>0,m<1<n,由题设m≥0,n≤6,
则
,
解不等式组的解集是:1<a≤2;
若a<0,n<1<m,由题设n≥0,m≤6,
则
,
解得:-2≤a<1;
综上:a的取值范围是:-2≤a<0,0<a≤2.
 解:(1)如图,∵抛物线y=-x2+x+c与x轴交于A,B两点,点B的坐标为B(-2,0).
解:(1)如图,∵抛物线y=-x2+x+c与x轴交于A,B两点,点B的坐标为B(-2,0).所以,-(-2)2+(-2)+c=0,即-6+c=0,
解得,c=6.
则该抛物线解析式是y=-x2+x+6;
(2)由(1)知,该抛物线解析式是y=-x2+x+6.
易求C(0,6).
设直线BC的解析式为y=k1x+6(k1≠0),则-2k1+6=0,
解得k1=3,
∴直线BC的解析式为y=3x+6.
∵点P的横坐标为x(-2<x<0),
∴F(x,3x+6),P(x,-x2+x+6),
∴PF=-x2+x+6-(3x+6)
=-x2-2x.
∴S=S△BPF+S△PCF,
=
| 1 |
| 2 |
∵-2<x<0,
∴当x=-1时,S最大=1.
综上所述,S与x之间的函数关系式是S=-x2-2x[或S=-(x+1)2+1],S的最大值是1;
(3)由(1)知,该抛物线解析式是y=-x2+x+6.则A(3,0).易求C(0,6).
设直线AC的解析式为y=k2x+6(k1≠0),则3k2+6=0,
解得k2=-2,
∴直线AC的解析式为y=-2x+6.
由已知M(2-a,2a+2),易知,m≠n,2-a≠2a+2,则a≠0.
若a>0,m<1<n,由题设m≥0,n≤6,
则
|
解不等式组的解集是:1<a≤2;
若a<0,n<1<m,由题设n≥0,m≤6,
则
|
解得:-2≤a<1;
综上:a的取值范围是:-2≤a<0,0<a≤2.
点评:本题考查了二次函数的综合运用.关键是根据二次函数图象上点的坐标特征求得二次函数解析式,由“两点法”求直线解析式,根据平行于x轴直线上点的坐标特点,表示三角形的面积,根据二次函数的性质求最大值.本题还考查了分类讨论的思想.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
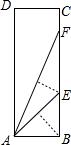 (2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则
(2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则 (2013•永春县质检)已知正比例函数y=x和反比例函数
(2013•永春县质检)已知正比例函数y=x和反比例函数