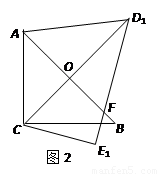题目内容
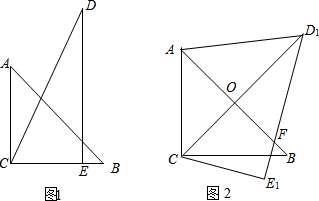
把两个三角形按如图1放置,其中![]() ,
,
![]() ,
,![]() ,且
,且![]() ,
,![]() .把△DCE
.把△DCE
绕点C顺时针旋转15°得到△D1CE1,如图2,这时AB与
CD1相交于点![]() ,与D1E1相交于点F.
,与D1E1相交于点F.
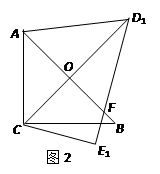 (1)求
(1)求![]() 的度数;
的度数;
(2)求线段AD1的长;
(3)若把△D1CE1绕点![]() 顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
(1)如图1,由题意可知:∠BCE1=15°,
∵∠D1CE1=60°,
∴∠D1CB=∠D1CE1—∠D1CB=45°,
又∠ACB=90°,
∴∠ACD1=∠ACB—∠D1CB=45°.····· 1分
(2)由(1)知,∠ACD1=45°,
又∠CAB=45°,
∴∠AOD1=∠CAB+∠ACD1=45°∴OC⊥AB,
∵∠BAC=45°,∠ABC=90°—∠BAC=45°,
∴∠ABC=∠BAC,∴AC=BC,
∴OC=![]() AB=OA=3,∴OD1=CD1—OC=4,
AB=OA=3,∴OD1=CD1—OC=4,
在Rt△AOD1中,∠5=90°,AD1=![]() =5.········ 3分
=5.········ 3分
(3)点B在△D2CE2内部.······················· 4分
理由如下:设BC(或延长线)交D2E2于点P,则∠PCE2=15°+30°=45°.
在Rt△PCE2中,可求CP=![]()
![]() CE2=
CE2=![]() ,
,
在Rt△ABC中,可求BC=![]() ,∵
,∵![]() ,即BC <CP,………5分
,即BC <CP,………5分
∴点B在△D2CE2内部.
解析:略

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目


 ,
,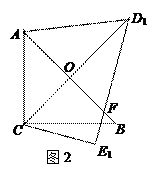
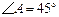 ,
,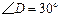 ,且
,且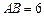 ,
,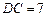 .把△DCE
.把△DCE ,与D1E1相交于点F.
,与D1E1相交于点F. 的度数;
的度数; 顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.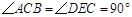 ,
,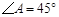 ,
,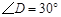 ,且
,且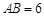 ,
,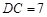 .把△DCE
.把△DCE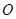 ,与D1E1相交于点F.
,与D1E1相交于点F.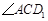 的度数;
的度数; 顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.