题目内容
【题目】如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒). 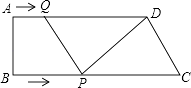
(1)当t为何值时,四边形PQDC是平行四边形.
(2)当t为何值时,以C、D、Q、P为顶点的梯形面积等于60cm2?
【答案】
(1)解:∵四边形PQDC是平行四边形,
∴DQ=CP,
当P从B运动到C时,如图1:

∵DQ=AD﹣AQ=16﹣t,
CP=21﹣2t
∴16﹣t=21﹣2t
解得:t=5
当P从C运动到B时,
∵DQ=AD﹣AQ=16﹣t,
CP=2t﹣21
∴16﹣t=2t﹣21,
解得:t= ![]() ,
,
∴当t=5或 ![]() 秒时,四边形PQDC是平行四边形
秒时,四边形PQDC是平行四边形
(2)解:若点P、Q分别沿AD、BC运动时,如图2:

![]() ×AB=60,
×AB=60,
即 ![]() ×12=60,
×12=60,
解得:t=9;
若点P返回时,CP=2(t﹣ ![]() ),
),
则  ×12=60,
×12=60,
解得:t=15.
故当t=9或15秒时,以C,D,Q,P为顶点的梯形面积等60cm2
【解析】(1)由题意已知,AD∥BC,要使四边形PQDC是平行四边形,则只需要让QD=PC即可,因为Q、P点的速度已知,AD、BC的长度已知,要求时间,用时间=路程÷速度,即可求出时间;(2)要使以C、D、Q、P为顶点的梯形面积等于60cm2,可以分为两种情况:点P、Q分别沿AD、BC运动或点P返回时,再利用梯形面积公式,即(QD+PC)×AB÷2=60,因为Q、P点的速度已知,AD、AB、BC的长度已知,用t可分别表示QD、BC的长,即可求得时间t.
【考点精析】利用平行四边形的判定与性质和梯形的定义对题目进行判断即可得到答案,需要熟知若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】将连续正整数按如下个规律排列
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ……… | |
第一行 | 1 | 2 | 3 | 4 | ||
第二行 | 8 | 7 | 6 | 5 | ||
第三行 | 9 | 10 | 11 | 12 | ||
第四行 | 16 | 15 | 14 | 13 | ||
第五行 | 17 | 18 | 19 | 20 | ||
……… |
若正整数2019位于第a行、第b列,则a+b=_____.
【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下: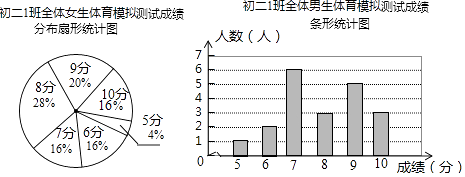
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根据以上信息,解答下列问题:
(1)这个班共有男生人,共有女生人;
(2)补全初二1班体育模拟测试成绩分析表;