��Ŀ����
����Ŀ���ۺ���ʵ��
�����Ķ� ������ǧ����ǰ���ҹ��ܳ���ѧ���̸߾��������һ��ֱ���۳�һ��ֱ�ǣ���������������ɵ����ģ���ô�Ҿ͵����壬�������������ģ��������������������ҹ��Ŵ�������ѧ�����������㾭���У�Ϊ�˷��㣬�ڱ����У����ǰ����ߵı�Ϊ3��4��5�������γ�Ϊ��3��4��5���������Σ����磺���߳��ֱ�Ϊ9��12��15��![]() �������ξ��ǣ�3��4��5���������Σ��þ���ֽƬ������IJ������������۳��������͵������Σ�
�������ξ��ǣ�3��4��5���������Σ��þ���ֽƬ������IJ������������۳��������͵������Σ�
ʵ������ ��ͼ1���ھ���ֽƬABCD�У�AD=8cm��AB=12cm��
��һ������ͼ2����ͼ1�еľ���ֽƬABCD�ع���A��ֱ���۵���ʹ��D����AB�ϵĵ�E�����ۺ�ΪAF������EF�۵���Ȼ���ֽƬչƽ��
�ڶ�������ͼ3����ͼ2�еľ���ֽƬ�ٴ��۵���ʹ��D���F�غϣ��ۺ�ΪGH��Ȼ��չƽ����ȥAF��
����������ͼ4����ͼ3�еľ���ֽƬ��AH�۵����õ���AD��H������AD���۵����ۺ�ΪAM��AM���ۺ�EF���ڵ�N��Ȼ��չƽ��

������
��1������ͼ2��֤���ı���AEFD�������Σ�
��2������ͼ4���ж�NF��ND����������ϵ��������֤����
��3������ͼ4��֤����AEN�ǣ�3��4��5���������Σ�
̽������
��4���ڲ�������ĸ������£�ͼ4�л�����Щ�������ǣ�3��4��5���������Σ����ҳ���ֱ��д�����ǵ����ƣ�
���𰸡���1��֤������������2��NF=ND����֤������������3��֤������������4����MFN����MD��H����MDA��
��������
�����������1����������������3��4��5���������εĶ���֤��������
��2��NF=ND����֤��Rt��HNF��Rt��HND�����ɣ�
��3����������������3��4��5���������εĶ���֤�����ɣ�
��4������AEN�ǣ�3��4��5���������Σ���������AEN���Ƶ������ǣ�3��4��5������������
�����������1�����ı���ABCD�Ǿ��Σ����D=��DAE=90�������۵�֪��AE=AD����AEF=��D=90�������D=��DAE=��AEF=90�������ı���AEFD�Ǿ��Σ���AE=AD��������AEFD�������Σ�
��2��NF=ND����֤�����£�
����HN�����۵�֪����AD��H=��D=90����HF=HD=HD����
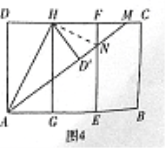
���ı���AEFD�������Σ����EFD=90����
�ߡ�AD��H=90�������HD��N=90����
��Rt��HNF��Rt��HND������HN=HN��HF=HD������Rt��HNF��Rt��HND������NF=ND����
��3�����ı���AEFD�������Σ���AE=EF=AD=8cm�����۵�֪��AD��=AD=8cm��EN=EF-NF=��8-x���M��
��Rt��AEN�У��ɹ��ɶ����ã�![]() ����
����![]() ����ã�x=2����AN=8+x=10���M����EN=6���M������AN=6��8��10=3��4��5�����AEN�ǣ�3��4��5���������Σ�
����ã�x=2����AN=8+x=10���M����EN=6���M������AN=6��8��10=3��4��5�����AEN�ǣ�3��4��5���������Σ�
��4������AEN�ǣ�3��4��5���������Σ���������AEN���Ƶ������ǣ�3��4��5���������Σ��ʴ�Ϊ����MFN����MD��H����MDA��

 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�����Ŀ��ѧУ����������Ϊ������ʷ����δ�������ݽ����������д����ߡ����꼶���������Ӹ�10�˵ı����ɼ����±���10���ƣ���
���꼶�� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
���꼶�� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
��1����ֱ��д�����꼶�ӳɼ�����λ��Ϊ �� ���꼶�ӳɼ�������Ϊ��
��2�����ߡ����꼶�ӵ�ƽ���ɼ���Ϊ9�֣���ֱ�����ߡ����꼶�ӵķ��