题目内容
【题目】如图,在平面直角坐标系中,点M(14,0)是x轴上的点,点P的坐标是(9,12),连接OP,PM. 
(1)求线段PM的长;
(2)在第一象限内找一点N,使四边形OPNM是平行四边形,画出图形并求出点N的坐标(保留作图痕迹)
【答案】
(1)解:过P点作PA⊥x轴于点A,
在Rt△PAM中,PA=12,AM=14﹣9=5,
则PM= ![]() =13
=13
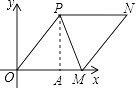
(2)解:如图所示:点N的坐标为(9+14=23,12),即(23,12)
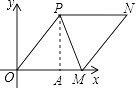
【解析】(1)过P点作PA⊥x轴于点A,在Rt△PAM中,根据勾股定理可求PM;(2)运用平行四边形性质,可知PN∥OM,所以点N的纵坐标是12,再根据OM间的距离即可推导出点N的横坐标,从而求解.
【考点精析】认真审题,首先需要了解平行四边形的判定(两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形).

练习册系列答案
相关题目