��Ŀ����
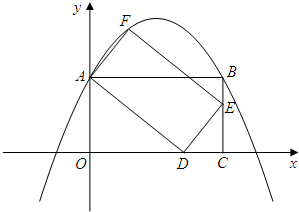
��ͼ��ƽ��ֱ������ϵ�У�����ABCO�ı�OA��y�������ϣ�OC��x�������ϣ���D���߶�OC��һ�㣬����D��DE��AD��ֱ��BC�ڵ�E����A��D��EΪ����������ADEF����1����֤����AOD�ס�DCE��
��2������A������0��4������C������7��0����
�ٵ���D������Ϊ��5��0��ʱ��������y=ax2+bx+c��A��F��B���㣬���F�����꼰a��b��c��ֵ��
������D��k��0�����߶�OC������һ�㣬��F�Ƿ��ڢ���������������ϣ�����ڣ���˵�����ɣ�������ڣ���ٷ���˵����
��3������A�������ǣ�0��m������C�������ǣ�n��0��������D���߶�OC���˶�ʱ���Ƿ�Ҳ����һ�������ߣ�ʹ�õ�F�����ڸ��������ϣ������ڣ���ֱ���ú�m
 ��n�Ĵ���ʽ��ʾ�������ߣ��������ڣ���˵�����ɣ�
��n�Ĵ���ʽ��ʾ�������ߣ��������ڣ���˵�����ɣ�
��������1�����ݡ�ECD=��ADE=��AOD=90�㣬�Լ���OAD=��EDC�����ɵó���AOD�ס�DCE��
��2���ɡ�AOD�ס�DCE���ó�CE=
��CD=2��������HF�ij�������A��0��4����F��2��
����B��7��4����������κ�������ʽ��
��3�����ݢ�ʽ��y=-
k2+
k+4��ֱ�ӽ�A��C���������뼴�ɣ�
��2���ɡ�AOD�ס�DCE���ó�CE=
| 5 |
| 2 |
| 13 |
| 2 |
��3�����ݢ�ʽ��y=-
| 1 |
| 4 |
| 7 |
| 4 |
���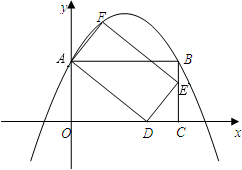 ��1��֤�������ı���ABCD�Ǿ��Σ�
��1��֤�������ı���ABCD�Ǿ��Σ�
���ECD=��ADE=��AOD=90�㣬
���ADO+��EDC=90�㣬
��OAD+��ADO=90�㣬
���OAD=��EDC��
���AOD�ס�DCE��
��2���⣺�ٹ�F��FH��OC��OC��H����AB��N��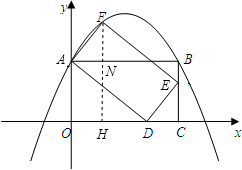
������ã�AB=OC=7��AO=BC=4��OD=5
�ߡ�AOD�ס�DCE��
��
=
��
��
=
��
��CE=
��CD=2
���ı���ADEF�Ǿ��Σ�DE=AF����DAB+��BAF=90��
�֡ߡ�OAD+��DAB=90�㣬
���OAD=��BAF��
���EDC=��BAF��
���AFN�ա�DEC��
��AN=DC=2��FN=EC=
��
��FH=
��F��������ǣ�2��
����
��A��0��4����F��2��
����B��7��4����
��
��
���
��
���A��F��B����������ߵı���ʽΪ��y=-
x2+
x+4��
�ڵ�F�ڢ���������������ϣ�
�����ǣ��ɣ�2���Тٿ�֪��
�����ߵı���ʽΪ��y=-
x2+
x+4��
��D��k��0��ʱ����DC=7-k��
ͬ�����ɡ�AOD�ס�DCE�͡�AFN�ա�DEC
��ã�F��7-k��4+
����
��x=7-k����y=-
x2+
x+4�ã�y=-
k2+
k+4��
��4+
=-
k2+
k+4
���Ե�F�ڢ���������������ϣ�
��3���⣺����һ�������ߣ�ʹ�õ�F�����ڸ��������ϣ�
�������ߵı���ʽΪ��y=-
x2+
x+m��
 ��1��֤�������ı���ABCD�Ǿ��Σ�
��1��֤�������ı���ABCD�Ǿ��Σ����ECD=��ADE=��AOD=90�㣬
���ADO+��EDC=90�㣬
��OAD+��ADO=90�㣬
���OAD=��EDC��
���AOD�ס�DCE��
��2���⣺�ٹ�F��FH��OC��OC��H����AB��N��

������ã�AB=OC=7��AO=BC=4��OD=5
�ߡ�AOD�ס�DCE��
��
| OD |
| CE |
| AO |
| CD |
��
| 5 |
| CE |
| 4 |
| 2 |
��CE=
| 5 |
| 2 |
���ı���ADEF�Ǿ��Σ�DE=AF����DAB+��BAF=90��
�֡ߡ�OAD+��DAB=90�㣬
���OAD=��BAF��
���EDC=��BAF��
���AFN�ա�DEC��
��AN=DC=2��FN=EC=
| 5 |
| 2 |
��FH=
| 13 |
| 2 |
��F��������ǣ�2��
| 13 |
| 2 |
��A��0��4����F��2��
| 13 |
| 2 |
��
|
���
|
���A��F��B����������ߵı���ʽΪ��y=-
| 1 |
| 4 |
| 7 |
| 4 |
�ڵ�F�ڢ���������������ϣ�
�����ǣ��ɣ�2���Тٿ�֪��
�����ߵı���ʽΪ��y=-
| 1 |
| 4 |
| 7 |
| 4 |
��D��k��0��ʱ����DC=7-k��
ͬ�����ɡ�AOD�ס�DCE�͡�AFN�ա�DEC
��ã�F��7-k��4+
| k(7-k) |
| 4 |
��x=7-k����y=-
| 1 |
| 4 |
| 7 |
| 4 |
| 1 |
| 4 |
| 7 |
| 4 |
��4+
| k(7-k) |
| 4 |
| 1 |
| 4 |
| 7 |
| 4 |
���Ե�F�ڢ���������������ϣ�
��3���⣺����һ�������ߣ�ʹ�õ�F�����ڸ��������ϣ�
�������ߵı���ʽΪ��y=-
| 1 |
| m |
| n |
| m |
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ����������ε��ж������ʣ���Ҫ����ѧ�����ν�ϵ���ѧ˼�뷽������һ���ѶȽϴ�Ķ��κ����⣬�ۺϿ��������������Ƶ����ʣ�

��ϰ��ϵ�д�
 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
�����Ŀ
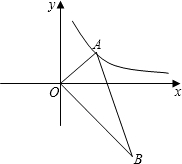 ��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫����
��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫����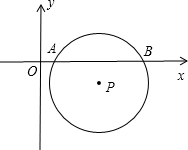 =2
=2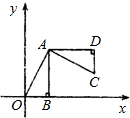 ��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ��������
��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ��������
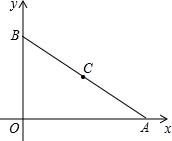 ��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�