题目内容
在梯形ABCD中,AD∥BC,AD=8cm,BC=2cm,AB=CD=6cm.动点P、Q同时从A点出发,点P沿线段AB→BC→CD的方向运动,速度为2cm/s;点Q沿线段AD的方向运动,速度为1cm/s.当P、Q其中一点先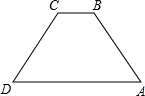 到达终点D时,另一点也随之停止运动.设运动时间为t(s),△APQ的面积为S(cm2).
到达终点D时,另一点也随之停止运动.设运动时间为t(s),△APQ的面积为S(cm2).(1)当点P在线段AB上运动时,是否存在某个t的值使∠CQP=60°?通过计算说明;
(2)当点P在CD上时,是否存在某个t的值使PQ=AQ?若存在,求出t的值;若不存在,请说明理由;
(3)试探究:点P在整个运动过程中,当t取何值时,S的值最大?并求出最大值.
分析:(1)若假设存在某个t的值使∠CQP=60°,则过 B作BE⊥AD于E,CF⊥ADAD于F,可证明△CDQ∽△AQP,利用相似的性质得到对应边的比值相等,建立关于t的方程,从而求出t,再求出t的取值范围,看是否满足题意即可;
(2)过点C作CE⊥AD于点E,构造直角三角形PDF和PFQ,利用已知条件和勾股定理建立建立关于t的方程,从而求出t的值;
(3)要根据点P在不同的时间段,即t的不同取值分三种情况进行分类讨论.
(2)过点C作CE⊥AD于点E,构造直角三角形PDF和PFQ,利用已知条件和勾股定理建立建立关于t的方程,从而求出t的值;
(3)要根据点P在不同的时间段,即t的不同取值分三种情况进行分类讨论.
解答: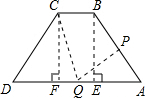 解:(1)不存在,
解:(1)不存在,
过B作BE⊥AD于E,CF⊥AD于F,
∵AD=8cm,BC=2cm,AB=CD=6cm,
∴AE=DF=3cm,
∴cosA=
=
=
,
∴∠A=∠D=60°,
若∠CQP=60°,则∠CQD+∠AQP=120°,
∵∠DCQ+∠CQD=120°,
∴∠DCQ=∠AQP,
∴△CDQ∽△AQP,
∴
=
,
∵AP=2t AQ=tDQ=8-t,
∴
=
,
∴t1=0,t2=-4,
∵点P在线段AB上运动
∴0<t<3
∴不存在某个t的值使∠CQP=60°.
(2)存在,过点P作PF⊥AD于F,
∵PD=14-2t,
∴PF=PD•sinD=(14-2t)•
=-
t+7
.
∴DF2=PD2-PF2=(14-2t)2-(-
t+7
)2
又∵FQ=8-AQ-DF
∴PQ2=PF2+FQ2
∴t=
∴当点P在CD上时,存在某个t的值使PQ=AQ.
(3)当点P在线段CD上(不与D点重合)时,4≤t<7.
过点P作PF⊥AD于F,如图.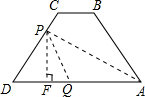
∵PD=14-2t,
∴PF=PD•sinD=(14-2t)•
=-
t+7
.
∴S=
•t(-
t+7
)=-
t2+
t(4≤t<7).
①∵当0<t≤3时.S=
t2.
由函数图象可知,S随t的增大而增大,
∴当t=3时,S最大=
;
②当3≤t≤4时,S=
t.
由函数图象可知,S随t的增大而增大,
∴当t=4时,S最大=6
;
③当4≤t<7时,S=-
t2+
t.
由函数图象知,S随t的增大而减小,
∴当t=4时,S最大=6
.(13分)
综上所述,在整个运动过程中,当t=4时,S的值最大.
 解:(1)不存在,
解:(1)不存在,过B作BE⊥AD于E,CF⊥AD于F,
∵AD=8cm,BC=2cm,AB=CD=6cm,
∴AE=DF=3cm,
∴cosA=
| AE |
| AB |
| 3 |
| 6 |
| 1 |
| 2 |
∴∠A=∠D=60°,
若∠CQP=60°,则∠CQD+∠AQP=120°,
∵∠DCQ+∠CQD=120°,
∴∠DCQ=∠AQP,
∴△CDQ∽△AQP,
∴
| CD |
| AQ |
| DQ |
| AP |
∵AP=2t AQ=tDQ=8-t,
∴
| 6 |
| t |
| 8-t |
| 2t |
∴t1=0,t2=-4,
∵点P在线段AB上运动
∴0<t<3
∴不存在某个t的值使∠CQP=60°.
(2)存在,过点P作PF⊥AD于F,
∵PD=14-2t,
∴PF=PD•sinD=(14-2t)•
| ||
| 2 |
| 3 |
| 3 |
∴DF2=PD2-PF2=(14-2t)2-(-
| 3 |
| 3 |
又∵FQ=8-AQ-DF
∴PQ2=PF2+FQ2
∴t=
21-
| ||
| 2 |
∴当点P在CD上时,存在某个t的值使PQ=AQ.
(3)当点P在线段CD上(不与D点重合)时,4≤t<7.
过点P作PF⊥AD于F,如图.

∵PD=14-2t,
∴PF=PD•sinD=(14-2t)•
| ||
| 2 |
| 3 |
| 3 |
∴S=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
7
| ||
| 2 |
①∵当0<t≤3时.S=
| ||
| 2 |
由函数图象可知,S随t的增大而增大,
∴当t=3时,S最大=
9
| ||
| 2 |
②当3≤t≤4时,S=
3
| ||
| 2 |
由函数图象可知,S随t的增大而增大,
∴当t=4时,S最大=6
| 3 |
③当4≤t<7时,S=-
| ||
| 2 |
7
| ||
| 2 |
由函数图象知,S随t的增大而减小,
∴当t=4时,S最大=6
| 3 |
综上所述,在整个运动过程中,当t=4时,S的值最大.
点评:本题考查了等腰梯形的性质和二次函数的最值,还利用了解直角三角形的有关知识.注意处理第(3)小题要分三种情况讨论.

练习册系列答案
相关题目
 10、如图,在梯形ABCD中,若AB∥CD,BD=AD,∠BCD=110°,∠CBD=30°,则∠ADC=
10、如图,在梯形ABCD中,若AB∥CD,BD=AD,∠BCD=110°,∠CBD=30°,则∠ADC= 如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之.
如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之. 如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.
如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E. 如图,在梯形ABCD中,AD∥BC,AB=AD,BD=BC,∠A=100°,则∠BDC的度数为( )
如图,在梯形ABCD中,AD∥BC,AB=AD,BD=BC,∠A=100°,则∠BDC的度数为( )