题目内容
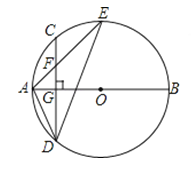
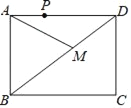
【题目】如图，矩形ABCD中，AB=2
，AD=6，P为边AD上一点，且AP=2，在对角线BD上寻找一点M，使AM+PM最小，则AM+PM的最小值为_____．
【答案】2
【解析】分析：作DH平分∠BDC交BC于H．连接AH交BD于M．首先证明P、H关于BD对称,连接AH交BD于M,则AM+PM的值最小,最小值=AH.
详解：作DH平分∠BDC交BC于H．连接AH交BD于M．
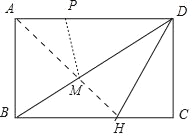
∵四边形ABCD是矩形，
∴∠C=∠BAD=∠ADC=90°，
∴tan∠ADB=
，
∴∠ADB=30°，
∴∠BDC=60°，
∴∠CDH=30°，
∵CD= AB=2
，
∴CH= tan30 ×2
2，
∴DH=2CH=4，
∴DP=DH，
∵∠MDP=∠MDH，
∴P、H关于BD对称，连接AH交BD于M，则AM+PM的值最小，最小值=AH=
．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某装修公司为某新建小区的A、B两种户型(共300套)装修地板
（1）若A种户型所需木地板、地板砖各为50m2、20m2，B种户型所需木地板、地板砖各为40m2、25m2．公司最多可提供木地板13000m2，最多可提供地板砖7010m2，在此条件下，则可能装修A、B两种户型各多少套？
（2）小王在该小区购买了一套A户型套房(地面总面积为70m2)．现有两种铺设地面的方案：①卧室铺实木地板，卧室以外铺亚光地板砖；②卧室铺强化木地板，卧室以外铺抛光地板砖．经预算，铺1m2地板的平均费用如下表．设卧室地面面积为am2，怎样选择所需费用更低？
类别 | 抛光地板砖 | 亚光地板砖 | 实木地板 | 强化木地板 |
平均费用（元/m2） | 170 | 90 | 200 | 80 |
